https://www.acmicpc.net/problem/7670
7670번: Game Dice
In the game of Dungeons & Dragons, players often roll multi-sided dice to generate random numbers which determine the outcome of actions in the game. These dice come in various flavors and shapes, ranging from a 4-sided tetrahedron to a 20-sided isocahedro
www.acmicpc.net
23/08/21
최근 확률 DP문제를 계속 공부하고 있다. 복습하고자 글로 남긴다.
문제 접근 방식:
DP로 접근했으며, DP테이블의 정의는 다음과 같다.
$$DP[i][j] = i번째 \ 주사위를 \ 던지고 \ 난 \ 후 \ 지금까지 \ 나온 \ 숫자의 \ 총 \ 합이 \ j일 \ 확률$$
$i$번째 주사위를 던지고 난 후와 $i-1$번째 주사위를 던지고 난 후의 관계를 시각화하면 다음과 같다고 할 수 있다.
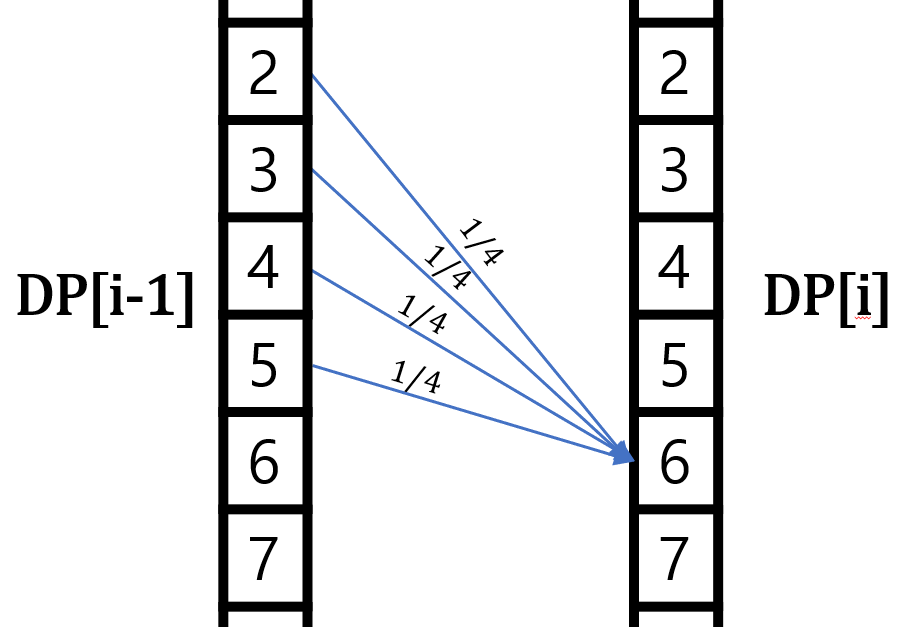
위의 그림은 $i$번째 주사위가 $d4$이고, 주사위를 굴렸을 때의 총합이 $6$일 때의 예시이다.
각 칸들($2, 3, 4, 5$)에서 주사위를 굴려서 $6$이 나올 확률은 모두 $1/4$로 동일함을 알고 있으므로, 이전 상태에서 다음 상태로 넘어갈 때에는 주사위가 나올 확률을 곱하고, 그 확률들을 모두 더해주면 된다.
따라서 DP점화식은 다음과 같다.
$$DP[i][j] = \sum DP[i][j'] * \textrm{dice probablity}$$
여기서 $j'$은 $i$번째 주사위를 굴렸을 때 총 합이 $j$가 될 수 있는 숫자이다.
위의 예시라면, $2, 3, 4, 5$가 $j'$에 해당할 것이다.
$0$번째 주사위를 굴려서 나오는 총 합의 확률은 $DP[0][1]$부터 $DP[0][\textrm{0th dice}]$까지 모두 $1/(\textrm{0th dice})$로 동일하므로, 이를 초기항으로 삼아주고 그대로 점화식을 구현하면 된다.
아래는 내가 위의 접근 방식과 같이 작성한 파이썬 코드이다. 더보기를 누르면 확인할 수 있다.
# 7670번 Game Dice
# DP, 확률론
import sys
input = sys.stdin.readline
def parsing(line):
line_li = line.split()
N = int(line_li[0])
dices = []
for dice in line_li[1:N+1]:
dices.append(int(dice[1:]))
x = int(line_li[N+1])
return N, dices, x
def solve(N, dices, x):
DP = [[0 for _ in range(1001)] for _ in range(N)]
for i in range(1, dices[0]+1):
DP[0][i] = 1/dices[0]
total_sum = dices[0]
for i in range(1, N):
dice = dices[i]
total_sum += dice
for j in range(total_sum+1):
for k in range(1, dice+1):
if j-k < 0:
break
DP[i][j] += DP[i-1][j-k]/dice
answer = f'{round(DP[N-1][x], 5):.5f}'
return answer
def main():
while True:
line = input().rstrip()
if line == '0':
return
print(solve(*parsing(line)))
main()'알고리즘 > 백준 문제 풀이' 카테고리의 다른 글
| [Python] 13255번 동전 뒤집기 (4) | 2023.08.24 |
|---|---|
| [Python] 12046번 Not So Random (Small) / 12047번 Not So Random (Large) (0) | 2023.08.23 |
| [Python] 1344번 축구 (0) | 2023.08.22 |
| [Python] 15488번 나이트가 체스판을 벗어나지 않을 확률 (0) | 2023.08.20 |
| [Python] 25280번 Marathon (0) | 2023.08.05 |



