https://www.acmicpc.net/problem/13255
13255번: 동전 뒤집기
첫째 줄에 동전의 개수 N (1 ≤ N ≤ 1,000)이 주어진다. 둘째 줄에는 K (1 ≤ K ≤ 50)이 주어진다. 셋째 줄에는 A[i] (1 ≤ A[i] ≤ N)가 주어진다.
www.acmicpc.net
23/08/23
최근 확률 DP 문제를 계속 공부하고 있다. 이 문제 또한 확률 DP 문제로 쉽게 해결할 수 있다.
또한, 약간의 최적화를 거치면 매우 빠르게 문제를 해결할 수 있다.
첫번째 접근 방식:
첫 번째로 접근한 방식은 나이브한 $3$차원 확률 DP이다.
DP테이블은 다음과 같이 정의했다.
$$DP[i][j][k] = i번째 \ 뒤집는 \ 행위를 \ 수행했을 \ 때 \ j번째 \ 동전이 \ k번 \ 뒤집혔을 \ 확률$$
$i-1$번째 뒤집는 행위를 했을 때의 확률과 $i$번째 뒤집는 행위를 했을 때의 확률 사이의 관계를 시각화해보면 다음과 같다.
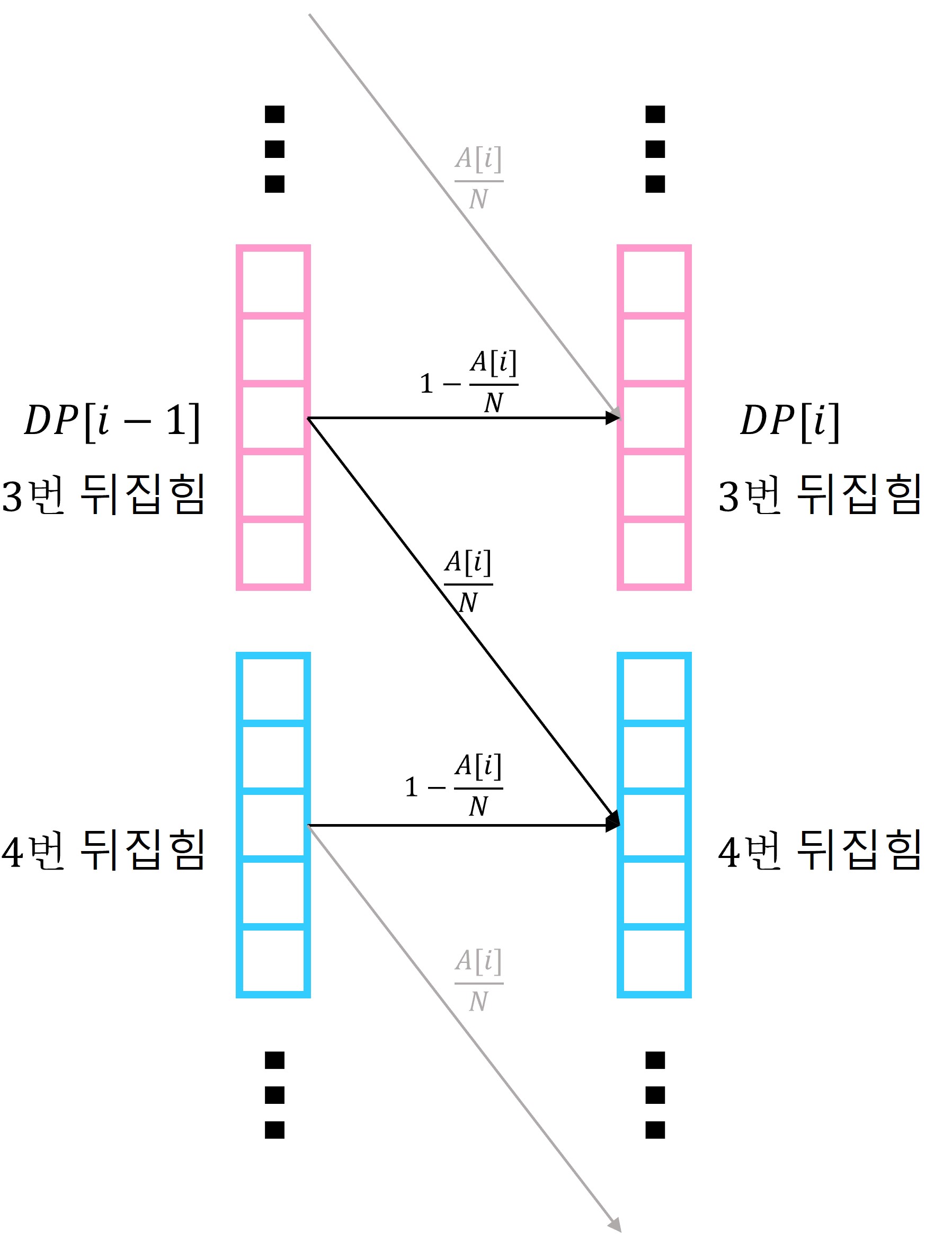
위의 그림은 동전이 $5$개 놓여져 있을 때의 예시이다.
$i-1$번째 상황에서 $i$번째 상황으로 넘어갈 때 특정한 동전이 뒤집힐 확률은 $A[i]/N$이다.
이때 동전이 뒤집힌다면 위의 그림과 같이 분홍색 노드는 하늘색 노드로, 하늘색 노드는 분홍색 노드로 간다는 사실을 알 수 있다.
그리고 이전 노드의 값에 동전이 뒤집힐 확률을 곱해서 다음 노드로 넘어갈 것이다.
또한, 특정한 동전이 뒤집히지 않을 확률은 $1 - A[i]/N$이므로 분홍색 노드에서 분홍색 노드로, 하늘색 노드에서 하늘색 노드로 갈 때에는 그 노드의 확률에 $1-A[i]/N$을 곱한 값이 다음 값이 된다.
최종적으로 나오는 점화식은 다음과 같다.
$$DP[i][j][k] = DP[i-1][j][k-1]*(A[i]/N) + DP[i-1][j][k]*(1-A[i]/N)$$
또한 아직 뒤집는 행위를 하지 않았을 때 모든 동전은 앞면이므로 이를 이용하여 초기항을 세우면 된다.
즉, $0$번째 뒤집는 행위를 수행했을 때 $j$번째 동전이 $0$번 뒤집혔을 확률은 $1$이다.
이를 초기항으로 삼고 DP를 돌리면 된다.
$K$는 최대 $50$이므로, 하나의 동전이 뒤집히는 최대 횟수는 $50$번이다.
따라서 DP테이블을 채우는 데에 소요되는 총 시간 복잡도는 $O(NK^2)$이다.
마지막에 동전이 앞면으로 있을 기댓값을 구하면 되므로, 즉, 마지막 뒤집는 시행까지 다 마친 후에 동전이 짝수 번 뒤집힐 확률들을 모두 더하면 기댓값을 구할 수 있다.
아래는 내가 위의 접근 방식과 같이 작성한 파이썬 코드이다. 더 보기를 누르면 확인할 수 있다.
# 13255번 동전 뒤집기
# DP, 확률론
'''
접근 방법:
DP[i][j][k] = i번 뒤집는 행위를 수행했을 때 j번째 동전이 k번 뒤집혔을 확률
DP[i][j][k] = DP[i-1][j][k-1]*뒤집힐 확률 + DP[i-1][j][k]*뒤집히지 않은 확률
'''
import sys
input = sys.stdin.readline
N = int(input())
K = int(input())
DP = [[[0 for _ in range(K+1)] for _ in range(N)] for _ in range(K+1)]
A = list(map(int, input().rstrip().split()))
# 초기항 설정
for j in range(N):
DP[0][j][0] = 1
# 점화식 구현
for i in range(1, K+1):
p = A[i-1]/N
for j in range(N):
DP[i][j][0] = DP[i-1][j][0]*(1-p)
for k in range(1, K+1):
DP[i][j][k] = DP[i-1][j][k-1]*p + DP[i-1][j][k]*(1-p)
# 기댓값 구하기
E = 0
for j in range(N):
for k in range(0, K+1, 2):
E += DP[K][j][k]
print(f'{E:.15f}')
두 번째 접근 방식:
첫 번째 접근 방식을 조금 생각해 보면, 우리는 DP의 점화식이 특정 동전끼리 서로 간섭하지 않는다는 사실을 알 수 있다.
또한 동전이 뒤집힐 확률은 뒤집는 모든 시행마다 $A[i]/N$으로 같으므로, 우리는 굳이 기댓값을 구할 때 $3$차원으로 할 이유가 없다.
즉, 특정 동전에 대한 확률만 구해도 그 확률이 모든 동전에 대해 성립되므로, 하나의 동전에 대해서만 DP 점화식을 생각해 줘도 된다.
이후에 그 확률에 $N$을 곱하면 충분하다.
이로써 차원이 하나 줄어들었다.
또한, 우리는 결국 동전이 "앞면"으로 있거나 "뒷면"으로 있거나 둘 중 하나의 상태로만 존재하다는 것을 알고 있다.
이를 이용한다면 굳이 동전이 $5$번, $6$번, $7$번 등 몇 번 뒤집혔는지 카운트하지 않아도 된다.
이를 시각화하면 다음 그림과 같다.

결국 차원은 하나 더 줄어들게 된다.
결국, 남는 차원은 하나밖에 없고, 이마저도 이전 상태와 현재 상태를 나타내는 관계식이므로 우리는 이를 "토글링"으로 빠르게 구현할 수 있다.
즉, 위의 그림을 점화식으로 나타내면 다음과 같다.
$$P \leftarrow P(1-p) + (1-P)p \textrm{ (where } p = A[i]/N)$$
여기서 $P$는 특정 동전이 짝수 번 뒤집힐 확률이다.
이를 $K$번 반복해 주고, 기댓값은 여기에 $N$을 곱해주면 구할 수 있다.
최종적인 시간 복잡도는 $O(K)$이다.
아래는 내가 위의 접근 방식과 같이 작성한 파이썬 코드이다. 더 보기를 누르면 확인할 수 있다.
import sys
input = sys.stdin.readline
N = int(input())
K = int(input())
A = list(map(int, input().rstrip().split()))
coin_probablity = 1
for a_i in A:
p = a_i/N
coin_probablity = coin_probablity*(1-p) + (1-coin_probablity)*p
E = coin_probablity*N
print(f'{E:.15f}')
'알고리즘 > 백준 문제 풀이' 카테고리의 다른 글
| [Python] 26074번 곰곰이와 테트리스 (2) | 2023.08.31 |
|---|---|
| [Python] 6068번 시간 관리하기 / 1263번 시간 관리 / 7983번 내일 할거야 (0) | 2023.08.30 |
| [Python] 12046번 Not So Random (Small) / 12047번 Not So Random (Large) (0) | 2023.08.23 |
| [Python] 7670번 Game Dice (0) | 2023.08.22 |
| [Python] 1344번 축구 (0) | 2023.08.22 |


