https://www.acmicpc.net/problem/1344
1344번: 축구
홍준이는 축구 경기를 보고 있다. 그러다가 홍준이는 역시 두 팀 중 적어도 한 팀이 골을 소수로 득점할 확률이 궁금해 졌다. 축구 경기는 90분동안 이루어지고, 분석을 쉽게하기 위해서 경기를 5
www.acmicpc.net
23/08/21
또 다른 확률 DP문제이다. 복습해 보고자 글을 작성한다.
첫 번째 접근 방식:
첫 번째 접근 방식은 확률 DP이다.
나는 다음과 같이 DP테이블을 정의하였다.
$$DP[i][j][k] = i번째 \ 구간에서 \ j번째 \ 팀이 \ k점이 \ 될 \ 확률$$
팀은 $2$팀 밖에 없고, 각 팀이 점수를 얻는 데에는 서로가 서로에게 간섭하지 않으므로, 우리는 한 팀에 대해서만 생각해도 충분하다.
한 구간에서 점수를 얻을 수 있을 확률을 $\textrm{Get score}$이라고 한다면, 한 구간에서 점수를 얻지 못할 확률은 $1 - \textrm{Get score}$이다.
이 확률을 $\textrm{No score}$이라고 해보자.
아래 그림은 $i-1$번째 구간과 $i$번째 구간 사이의 관계를 시각화하여 나타낸 것이다.
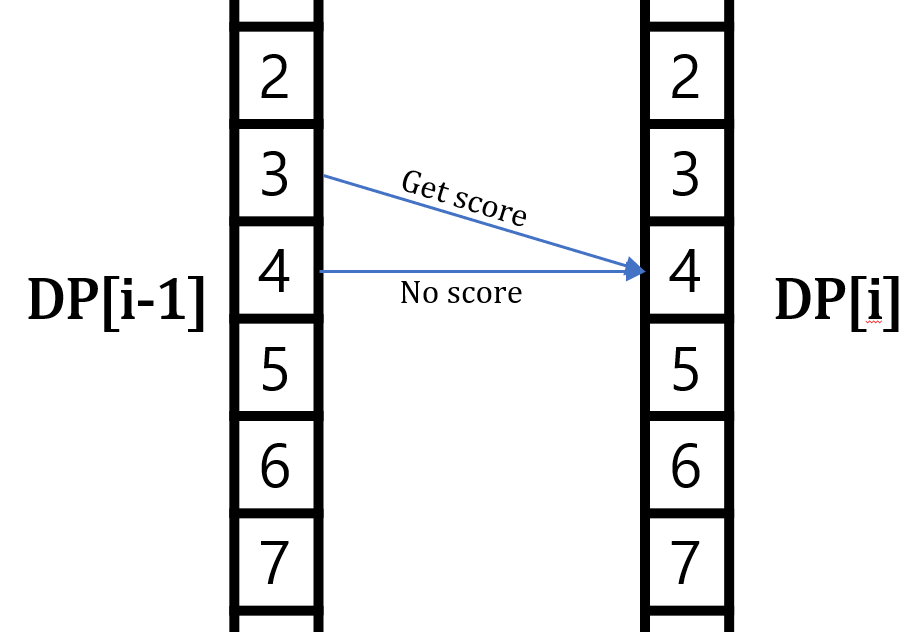
이 그림을 통해 알 수 있는 DP관계식은 다음과 같다.
$$DP[i][j][k] = DP[i-1][j][k-1]*\textrm{Get score} + DP[i-1][j][k]*\textrm{No score}$$
초기 항을 설정해주어야하는데, 즉, $0$번째 구간에서 점수를 얻을 확률을 설정해주어야 한다.
$0$번째 구간에서 가능한 점수는 $0$점이거나 $1$점 밖에 없으므로, 초기항은 다음과 같이 설정할 수 있다.
$$DP[0][j][0] = \textrm{No score}, DP[0][j][1] = \textrm{Get score}$$
그 외에는 모두 $0$으로 설정해주면 된다.
또한 경기는 $90$분을 진행하므로, 구간의 개수가 $18$개라는 사실을 알 수 있다.
따라서 한 팀이 얻을 수 있는 최대 점수는 $18$점이다.
우리는 경기가 종료되었을 때, 즉, 한 팀이 마지막 구간에 도달했을 때 소수인 점수를 얻을 수 있는 확률을 구해야 한다.
이 확률은 $18$이하의 소수, 즉, 마지막 구간 때 $2, 3, 5, 7, 11, 13, 17$점이 되는 확률을 모두 더해주면 구할 수 있다.
그렇게 해서 각 팀 별로 구한 확률을 $A, B$라고 하자.
최종적으로 우리가 원하는 확률은 적어도 한 팀이 소수인 점수를 얻을 확률이다.
즉, 전체 확률에서 두 팀 모두가 소수인 점수를 얻지 못할 확률을 뺀 값이다.
두 팀 모두가 소수인 점수를 얻지 못할 확률은, $(1-A)(1-B)$이므로, 최종적으로 우리가 원하는 확률은 $1 - (1-A)(1-B)$라고 할 수 있다.
아래는 내가 위의 접근 방식과 같이 작성한 파이썬 코드이다. 더 보기를 누르면 확인할 수 있다.
# 1344번 축구
# 확률론, DP
'''
접근 방법:
DP[i][j][k] = i번째 구간에서 j번째 팀이 k점이 될 확률
간격은 5분 간격이고 총 90분이기 때문에 18개의 간격으로 쪼개진다는 것을 알 수 있다.
최대 18점을 획득할 수 있다는 사실을 알 수 있다.
점화식은 다음과 같다.
DP[i][j][k] = DP[i-1][j][k-1]*득점할 확률 + DP[i-1][j][k]*득점하지 못할 확률
초기 항은 다음과 같다.
DP[0][j][0] = 득점하지 못할 확률
DP[0][j][1] = 득점할 확률
그외에는 0
소수는 2, 3, 5, 7, 11, 13, 17
따라서 17번째 구간에서 2, 3, 5, 7, 11, 13, 17점이 될 확률을 모두 더하면 된다.
'''
import sys
input = sys.stdin.readline
DP = [[[0 for _ in range(19)] for _ in range(2)] for _ in range(18)]
a = int(input())/100
b = int(input())/100
DP[0][0][0], DP[0][0][1] = 1-a, a
DP[0][1][0], DP[0][1][1] = 1-b, b
for i in range(1, 18):
for j in range(2):
if j == 0:
for k in range(19):
DP[i][j][k] = DP[i-1][j][k-1]*a + DP[i-1][j][k]*(1-a)
else:
for k in range(19):
DP[i][j][k] = DP[i-1][j][k-1]*b + DP[i-1][j][k]*(1-b)
primes = [2, 3, 5, 7, 11, 13, 17]
team_a_probablity_that_scores_primes = 0
team_b_probablity_that_scores_primes = 0
for prime in primes:
team_a_probablity_that_scores_primes += DP[17][0][prime]
team_b_probablity_that_scores_primes += DP[17][1][prime]
answer = 1 - (1-team_a_probablity_that_scores_primes)*(1-team_b_probablity_that_scores_primes)
print(answer)
두 번째 접근 방식:
이후 기여창을 확인한 뒤에, 이 문제를 수학적으로 풀 수 있다는 사실을 알게 되었다.
$18$번의 구간이 있고, 각 구간마다 점수를 얻을 확률은 모두 동일하므로, 이항분포의 확률질량함수를 생각할 수 있다.
쉽게 이야기하자면, 각 구간마다 점수를 얻거나 얻지 못하거나 둘 중 하나를 "선택"한다고 생각하면 된다.
점수를 얻을 확률을 $p$라고 한다면, 점수를 얻지 못할 확률은 $1-p$이다.
따라서 $18$번의 구간을 거치고 났을 때, 점수가 $x$점이 될 확률은 $_{18}\mathrm{C}_{x} p^x (1-p)^{18-x}$이고, 조합은 파이썬 math모듈의 comb함수로 쉽게 구할 수 있으므로, 이를 통해 위에서 이야기 한 $A$와 $B$를 구하면 된다.
아래는 내가 위의 접근 방식과 같이 작성한 파이썬 코드이다. 더 보기를 누르면 확인할 수 있다.
'''
접근 방법:
확률질량함수 이용
'''
import sys
input = sys.stdin.readline
from math import comb
primes = [2, 3, 5, 7, 11, 13, 17]
a = int(input())/100
b = int(input())/100
team_a_probablity_that_scores_primes = 0
team_b_probablity_that_scores_primes = 0
for prime in primes:
team_a_probablity_that_scores_primes += comb(18, prime)*(a**prime)*((1-a)**(18-prime))
team_b_probablity_that_scores_primes += comb(18, prime)*(b**prime)*((1-b)**(18-prime))
answer = 1 - (1-team_a_probablity_that_scores_primes)*(1-team_b_probablity_that_scores_primes)
print(answer)'알고리즘 > 백준 문제 풀이' 카테고리의 다른 글
| [Python] 12046번 Not So Random (Small) / 12047번 Not So Random (Large) (0) | 2023.08.23 |
|---|---|
| [Python] 7670번 Game Dice (0) | 2023.08.22 |
| [Python] 15488번 나이트가 체스판을 벗어나지 않을 확률 (0) | 2023.08.20 |
| [Python] 25280번 Marathon (0) | 2023.08.05 |
| [Python] 24838번 배열 구간합 놀이 (0) | 2023.08.05 |


