https://www.acmicpc.net/problem/15488
15488번: 나이트가 체스판을 벗어나지 않을 확률
첫째 줄에 N, 나이트의 좌표 x, y, 이동 횟수 K가 주어진다. (1 ≤ N ≤ 50, 1 ≤ x, y ≤ N, 0 ≤ K ≤ 50)
www.acmicpc.net
23/08/18
확률DP 문제로, 이 유형을 처음 접해봤기 때문에 복습을 해보고자 글을 작성한다.
첫 번째 접근 방식:
처음 접근 방식은 BFS를 구현하여 직접 나이트를 옮기면서 나올 수 있는 확률들을 모두 곱하는 방식이었다.
이 방식은 다음과 같다.
우리는 나이트가 $K$번 이동한다는 사실을 알고 있고, 나이트가 체스판을 벗어나는 이동을 하는 순간, 그 즉시 더 이상 움직일 수 없다는 것 또한 알고 있다.
기본적인 방법은 BFS이기 때문에 현재 나이트가 있는 위치를 저장하는 리스트 $\textrm{knight in board}$를 선언하여, 이 리스트에 현재 나이트가 있는 위치 $(x, y)$를 저장해 주었다.
이후 for문으로 $K$번 반복하며 다음과 같은 행동을 취해주었다.
- 나이트가 다음에 있을 수 있는 위치를 저장하는 리스트 $\textrm{new li}$와 나이트가 보드를 벗어나는 경우를 세어주는 변수 $\textrm{knight out board}$를 선언해 준다.
- 이후 $\textrm{knight in board}$에서 하나씩 현재의 위치를 꺼내서 이 위치에서 $8$방향 BFS를 돌린다.
- 만약 BFS를 통해 갈 수 있는 위치라면 $\textrm{new li}$에 담아주고, 그렇지 않으면 $\textrm{knight out board}$에 $1$을 더해준다.
- (갈 수 있는 경우의 수) $/$ (전체 경우의 수)를 계산해 준다. 즉, $\textrm{len(new li)} / ( \textrm{len(new li)} + \textrm{knight out board} )$를 계산한다. 이 확률을 지금까지의 확률에 곱해준다. 분모가 $0$이 되는 예외처리 또한 진행한다.
이 과정을 다 거치면 최종적으로 나오는 확률이 답이 된다.
아래는 내가 위의 접근 방식과 같이 작성한 파이썬 코드이다. 더 보기를 누르면 확인할 수 있다.
# 15488번 나이트가 체스판을 벗어나지 않을 확률
# BFS, 확률론
import sys
from fractions import Fraction
input = sys.stdin.readline
N, x, y, K = map(int, input().rstrip().split())
dr = [1, 2, 2, 1, -1, -2, -2, -1]
dc = [2, 1, -1, -2, -2, -1, 1, 2]
probablity = Fraction(1)
knight_in_board = [(x, y)]
knight_out_board = 0
for _ in range(K):
new_li = []
while knight_in_board:
x, y = knight_in_board.pop()
for i in range(8):
nx, ny = x+dr[i], y+dc[i]
if 1 <= nx <= N and 1 <= ny <= N:
new_li.append((nx, ny))
else:
knight_out_board += 1
if new_li == []:
probablity = 0
break
probablity *= Fraction(len(new_li), len(new_li)+knight_out_board)
knight_in_board = new_li
knight_out_board = 0
print(float(probablity))
두 번째 접근 방식:
첫 번째 풀이 방식으로 접근을 하여 문제를 푸니 입력이 $N = 50$만 되어도 매우 오랜 시간이 걸린다는 점을 알 수 있었다.
또한, 첫번째 풀이를 제출을 해보니 메모리 초과가 나서 다른 풀이 방식을 생각해야 했었다.
같이 공부하는 그룹원들의 도움을 받아, DP로 문제 접근 방식을 틀었다.
DP 테이블의 정의는 다음과 같다.
$$DP[z][x][y] = 지금까지 \ z번 \ 움직여서 \ (x, y)에 \ 있을 \ 확률$$
이를 이용하여 다음 그림과 같이 $DP[z-1]$과 $DP[z]$의 관계를 시각화해보았다.
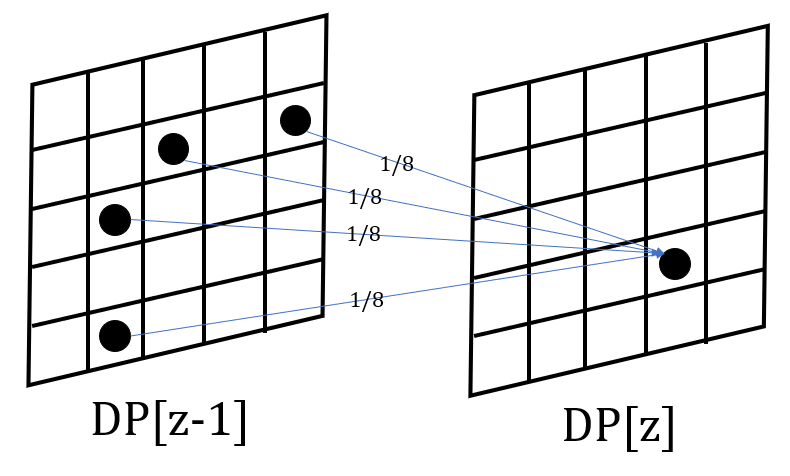
한 지점으로 갈 수 있으려면, 이전에 내가 있는 위치가 BFS를 통해 갈 수 있는 지점이어야 한다.
우리는 $8$방향으로 "고르게"가므로, 한 지점에서 다른 지점으로 갈 때에는 확률에 $1/8$을 곱해주어야 한다.
따라서 다음과 같은 점화식을 만들 수 있다.
$$DP[z][x][y] = \mathrm{sum}(DP[z-1][x'][y'] / 8)$$
여기서 $(x', y')$은 한 번의 이동을 통해 $(x, y)$로 갈 수 있는 지점이다.
이를 그대로 DP로 구현하면 된다.
아래는 내가 위의 접근 방식과 같이 작성한 파이썬 코드이다. 더 보기를 누르면 확인할 수 있다.
# 15488번 나이트가 체스판을 벗어나지 않을 확률
# BFS, 확률론, DP
'''
접근 방법:
각 칸별로 벗어나지 않을 확률을 저장한다
'''
import sys
input = sys.stdin.readline
N, x, y, K = map(int, input().rstrip().split())
dr = [1, 2, 2, 1, -1, -2, -2, -1]
dc = [2, 1, -1, -2, -2, -1, 1, 2]
DP = [[[0 for _ in range(N)] for _ in range(N)] for _ in range(K+1)]
DP[0][x-1][y-1] = 1
for p in range(1, K+1):
for i in range(N):
for j in range(N):
for k in range(8):
ni, nj = i+dr[k], j+dc[k]
if 0 <= ni < N and 0 <= nj < N:
DP[p][ni][nj] += DP[p-1][i][j]/8
ans = 0
for i in range(N):
for j in range(N):
ans += DP[K][i][j]
print(ans)'알고리즘 > 백준 문제 풀이' 카테고리의 다른 글
| [Python] 7670번 Game Dice (0) | 2023.08.22 |
|---|---|
| [Python] 1344번 축구 (0) | 2023.08.22 |
| [Python] 25280번 Marathon (0) | 2023.08.05 |
| [Python] 24838번 배열 구간합 놀이 (0) | 2023.08.05 |
| [Python] 24187번 Korta vokaler (0) | 2023.07.04 |

