https://www.acmicpc.net/problem/12046
12046번: Not So Random (Small)
The first line of the input gives the number of test cases, T. T test cases follow; each consists of one line with six integers N, X, K, A, B, and C. Respectively, these denote the number of machines, the initial input, the fixed number with which
www.acmicpc.net
https://www.acmicpc.net/problem/12047
12047번: Not So Random (Large)
The first line of the input gives the number of test cases, T. T test cases follow; each consists of one line with six integers N, X, K, A, B, and C. Respectively, these denote the number of machines, the initial input, the fixed number with which
www.acmicpc.net
23/08/22
Large 문제를 해결한 코드로 Small 그대로 통과했기 때문에 따로 분리해서 작성하지 않고 Large 코드로 접근한 방식만 설명할 것이다.
문제 접근 방식:
확률 DP를 최근에 계속 연습하고 있기 때문에 확률 DP로 문제를 접근하였다.
DP테이블의 정의는 다음과 같다.
$$DP[i][j] = 지금까지 \ 기계에 \ i번 \ 들어갔을 \ 때, \ j일 \ 확률$$
이 테이블의 정의를 통해 기계에 $i$번 들어갔을 때와 $i-1$번 들어갔을 때 사이의 관계를 시각화해보면 다음과 같다.
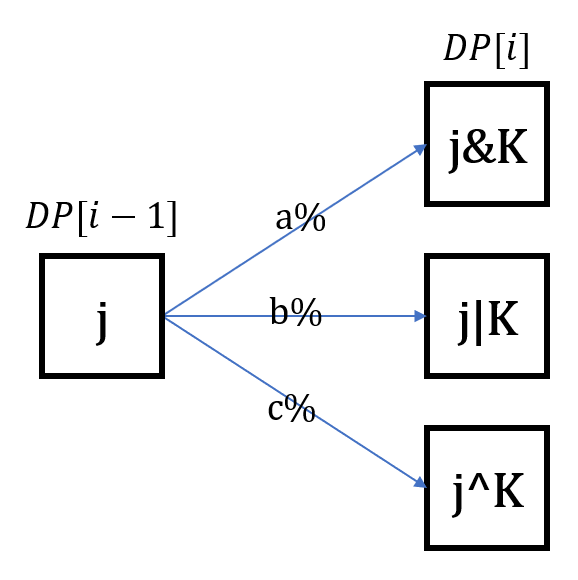
이를 통해 알 수 있는 점화식은 다음과 같다.
$$DP[i][j] = DP[i-1][j_a]*a/100 + DP[i-1][j_b]*b/100 + DP[i-1][j_c]*c/100$$
여기서 $j_a, j_b, j_c$는 각각에 $K$와 AND연산, OR연산, XOR연산을 하면 $j$가 되는 숫자들이다.
하지만 우리는 나올 수 있는 숫자의 범위가 $10^9$보다 크다는 사실을 알고 있고, $N$의 제한 또한 $10^5$로 매우 크기 때문에 DP테이블을 빈 $2$차원 리스트로 선언하면 매우 메모리 낭비가 심할 것이다.
왜냐하면 그중 대부분은 확률이 $0$일 것이기 때문이다.
따라서 나는 위의 점화식을 딕셔너리의 토글링으로 구현하였다.
또한, 원래라면 딕셔너리에 값이 없을 경우와 딕셔너리에 값이 있는 경우를 따져주어서 구현해주어야 하지만, 조금 귀찮기 때문에 collections모듈의 defaultdict를 이용하였다.
defaultdict는 값이 있으나 없으나 그냥 더해주어도 오류가 나지 않기 때문에 유용하다.
"기댓값"을 구하는 것이 우리의 목적이기 때문에, 마지막까지 거쳐서 나온 DP딕셔너리의 원소(숫자)와 그 값(확률)을 서로 곱해서 모두 더하면 최종 답이 된다.
매우 유의할 점은, 파이썬에서는 매우 작은 숫자가 나오거나 매우 큰 숫자가 나오면 지수표기법으로 숫자를 나타내기 때문에 의문의 틀렸습니다를 받을 수도 있다.
따라서 실수 포매팅으로 정해진 자릿수만큼 고정되어 출력하도록 구현해주어야 한다.
이것 때문에 의문의 틀렸습니다를 수없이 많이 받았다...
아래는 내가 위의 접근 방식과 같이 작성한 파이썬 코드이다. 더 보기를 누르면 확인할 수 있다.
# 12047번 Not So Random (Large)
# 확률론, DP
import sys
input = sys.stdin.readline
from collections import defaultdict
def parsing(line):
N, X, K, A, B, C = map(int, line.rstrip().split())
return N, X, K, A, B, C
def solve(N, X, K, A, B, C):
DP = defaultdict(int)
DP[X] = 1
for _ in range(N):
temp = defaultdict(int)
for num in DP:
temp[num&K] += DP[num]*A/100
temp[num|K] += DP[num]*B/100
temp[num^K] += DP[num]*C/100
DP = temp
return sum(num*DP[num] for num in DP)
def main():
T = int(input())
for i in range(1, T+1):
print(f'Case #{i}: {solve(*parsing(input())):.15f}')
main()'알고리즘 > 백준 문제 풀이' 카테고리의 다른 글
| [Python] 6068번 시간 관리하기 / 1263번 시간 관리 / 7983번 내일 할거야 (0) | 2023.08.30 |
|---|---|
| [Python] 13255번 동전 뒤집기 (2) | 2023.08.24 |
| [Python] 7670번 Game Dice (0) | 2023.08.22 |
| [Python] 1344번 축구 (0) | 2023.08.22 |
| [Python] 15488번 나이트가 체스판을 벗어나지 않을 확률 (0) | 2023.08.20 |


