https://www.acmicpc.net/problem/26074
26074번: 곰곰이와 테트리스
곰곰이가 첫 차례에 4번째 종류의 블록(2×2 모양)을 그림과 같이 배치하고 20점을 획득하면, 이후 게임이 어떻게 흘러가던 관련 없이 무조건 이길 수 있다.
www.acmicpc.net
23/08/24
이전에 곰곰컵 때 이 문제를 풀어보려고 시도했다가 실패했었다.
엄청난 전략이 숨어있는 문제로, 이 글을 보기 전에 충분한 고민을 하기 추천한다.
여담으로 내 1800번째 문제이다.
문제 접근 방식:
이 문제는 겉으로 볼 때 많은 것들을 고려해야 되는 것처럼 보인다.
블록 별로 점수가 다양하게 주어지고, 판의 크기 또한 다양하게 주어지는 상황 속에서 "최적의 행동"을 생각해야 하기 때문이다.
이 문제의 핵심은 게임의 승/패는 오로지 "판의 크기"에 따라 달려있다는 것이다.
겉보기에는 많은 것을 생각해야 되는 것 처럼 보이지만, 실제로는 판의 크기만 신경 쓰면 된다.
예를 들어, $1 \times 1$크기의 판을 생각해보자. 그렇다면, 선공(곰곰이)이 뭔 짓을 하든 무조건 이긴다.
블록의 점수는 모두 $1$점 이상이고, 선공 페널티로 깎이는 점수는 $0.5$점 밖에 되지 않기 때문이다.
만약 생각할 수 있는 일반적인 판의 모습이라면 어떻게 될까?
두 사람이 모두 "최적의 방법"으로 행동한다는 것이 이 문제의 핵심이다.
"최적의 방법"이라는 것은, 두 사람이 서로가 서로의 전략을 통찰하듯 모두 알고 있다는 것이다.

예를 들어, $2 \times 4$크기의 판이 주어져 있고, $1$번 블록부터 $7$번 블록의 점수는 모두 $1$점이고, $8$번 블록의 점수가 $20$점이라고 해보자.
"그리디"적으로 생각했을 때에는 $8$번 블록의 점수가 가장 높으니깐 다른 블록을 선택하는 건 최적이 아니다.
그러므로 선공(곰곰이)이 $8$번 블록을 선택하고, 후공(총총이)도 $8$번 블록을 선택해서 계속 놓다 보면 후공(총총이)이 마지막으로 놓게 된다.
선공(곰곰이)이 페널티로 $0.5$점이 깎이므로, 결국 후공(총총이)이 이기게 된다.
하지만, 이게 정말 최선의 결과일까?
선공(곰곰이)은 이렇게 $8$번 블록만 놓다보면 자신이 질 거라는 사실 또한 "이미 알고 있다."
따라서, 최대한 이런 상황을 피하려고 할 것이다.
그래서 곰곰이는 처음에 판의 남은 칸 수를 짝수개로 만들려고 할 것이다. 그러면 곰곰이가 이 게임에서의 실질적 후공으로 바뀌는 효과가 일어난다.
그러면 곰곰이는 $4$칸을 차지하는 블록(블록 $1$부터 블록 $7$)을 맨 처음에 둬야 할 것이다.
하지만, 이 또한 그냥 놓으면 안된다.
예를 들어, 다음과 같은 두 상황을 가정해 보자.
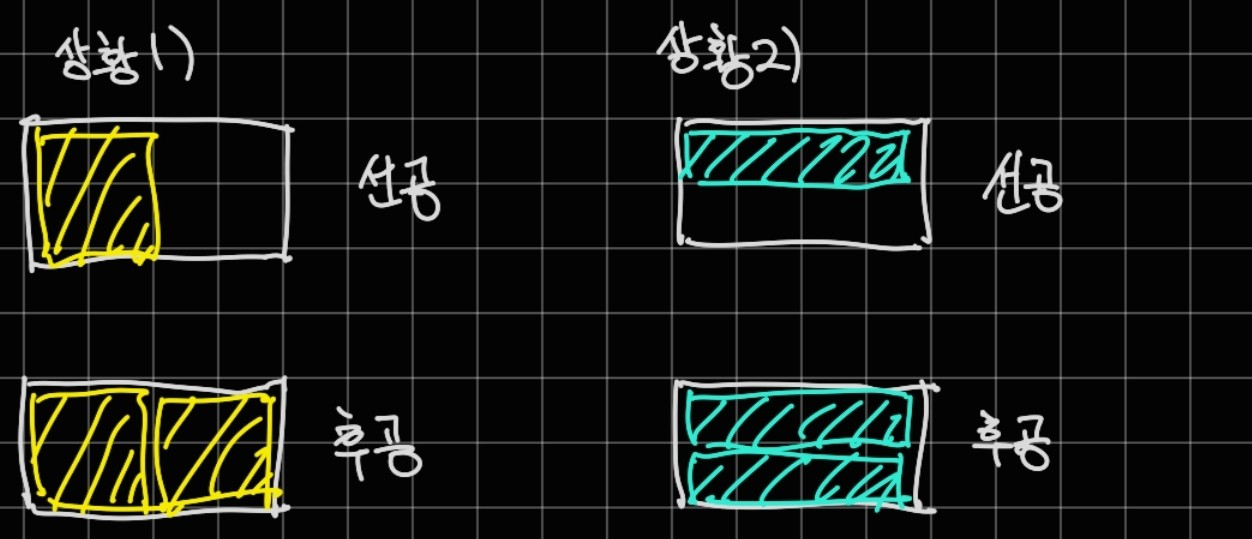
이 상황의 경우는 선공(곰곰이)이 자신의 선/후공을 바꾸기 위해 $4$칸짜리 블록을 놨음에도 불구하고 지는 경우다.
그 이유는, 후공(총총이)이 선공(곰곰이)이 놨던 자리에 "대칭적으로"놔서 선/후공을 바꾸려는 곰곰이의 노력이 의미가 없어졌기 때문이다.
하지만 상황 $3$과 같이 후공(총총이)이 대칭적으로 놓을 수 있는 상황을 방지한다면 이길 것이다.

이 경우에서는 후공(총총이)이 어떤 짓을 해도 선공(곰곰이)이 이길 수 있다.
따라서 우리는 $2 \times 4$크기의 판에서는 선공(곰곰이)이 항상 이길 것이라는 추측을 할 수 있다.
그리고 이는 각 블록별 점수와 "전혀" 무관하다.
우리는 여기서 상황 $3$의 선공(곰곰이)의 행동에 유의할 필요가 있다.
이 상황에서 선공(곰곰이)은 가운데에 블록을 놓음으로써 실질적 선/후공을 뒤바꾸고, 이후의 행동은 후공(총총이)의 행동을 따라 했다.
사실, 상황 $3$처럼 선공(곰곰이)이 선/후공을 뒤바꿀 수 있으면서, 이후에 상대방의 행동을 따라 할 수 있다면 게임에서 이길 수 있다.
왜냐하면, 상대방의 행동을 따라 한다는 건 결국 상대방이 얻은 점수만큼 나도 똑같은 점수를 얻는다는 뜻이기 때문이다.
그리고 후공(총총이)이 이러한 상황을 벗어나기 위해 $8$번 블록이나 다른 $4$칸짜리 블록을 특정 위치에 놓음으로써 선/후공을 다시 뒤바꾸려 해도, 혹은, 상대방(곰곰이)을 불리하게 만들려고 해도, 선공(곰곰이)은 후공(총총이)이 한 행동을 따라 하니 다시 원래 선공(곰곰이)이 유리했던 상태로 돌아갈 것이다.
또한, 블록으로 판을 메우다 보면 마지막에 놓는 사람은 곰곰이이다.(상황 $3$처럼 짝수 개의 칸이 남으면 선공(곰곰이)이 마지막으로 놓는다.)
하지만 선공(곰곰이)은 맨 처음에 블록 하나만큼을 더 놨으므로, 그만큼의 점수를 더 얻을 수 있다.
선공 페널티는 $0.5$점 밖에 불과하고, 블록은 최소 $1$점 이상의 점수를 지니니, 상황 $3$처럼 되어있는 경우라면 항상 선공(곰곰이)이 이길 수 있다고 말할 수 있다.
이러한 상황이 가능한 경우는 언제일까?
먼저, $(홀수) \times (홀수)$크기를 가진 판의 경우를 생각해 보자.

이 경우 상황 $3$에서 했던 것처럼 선공(곰곰이)이 한가운데에 $8$번 블록을 놓고, 이후 후공(총총이)이 놨던 곳에 대칭적으로 놓으면 선공(곰곰이)이 항상 이김을 알 수 있다.
$(짝수)\times (짝수)$의 경우라면 어떨까?
이는 상황 $3$처럼 한 가운데에 $4$번 블록을 놓고 이후 대칭적으로 놓으면 된다.
이제, $(홀수)\times (짝수)$의 경우만 남았다.
얼핏 봐서는 한가운데에 뭔가를 놔서 선/후공을 바꾸고 상황을 대칭적으로 만들기가 쉽지 않아 보인다.
하지만 다음과 같이 $7$번 블록이나 $5$번 블록을 활용하면 판의 모양을 대칭적으로 만들면서, 동시에 선/후공을 뒤바꿀 수 있다.

하지만, $7$번 블록이나 $5$번 블록을 놓을 수 없는 상황이라면 판의 모양을 대칭적으로 만들 수 없을 것이다.
즉, $1 \times 2$크기의 판이나 $2 \times 1$크기의 판일 때에는 판의 모양을 대칭적으로 만들 수 없다.
따라서 이때는 후공(총총이)이 이기게 된다.
결론을 요약하자면, $1 \times 2$크기나 $2 \times 1$크기의 판 일 때에만 후공(총총이)이 무조건 이기고, 그 외에는 선공(곰곰이)이 한가운데에 놓음으로써 실질적 선/후공을 뒤바꾸고, 이후에는 후공(총총이)이 놨던 곳에 선공(곰곰이)이 대칭적으로 놓음으로써 선공(곰곰이)이 이김을 알 수 있다.
여담으로, 위의 전략을 그대로 사용하는 퀴즈가 있다.
https://www.geeksforgeeks.org/puzzle-round-table-coin-game/
Puzzle | (Round table coin game) - GeeksforGeeks
A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions.
www.geeksforgeeks.org
이 문제는 위 퀴즈의 변형버전이다.
하지만 전략 자체는 따라쟁이 전략이므로, 게임이론의 유명한 전략 중 하나인 팃포탯과 비슷한 맥락이라고 생각할 수도 있을 것이다.
아래는 내가 위의 접근 방식과 같이 작성한 파이썬 코드이다. 더 보기를 누르면 확인할 수 있다.
# 26074번 곰곰이와 테트리스
# 게임이론
'''
접근 방법:
처음에 한가운데에 놓은 후 대칭으로 놓는다.
이게 가능하면 선공이 항상 이긴다.
'''
N, M = map(int, input().split())
input()
if (N, M) == (1, 2) or (N, M) == (2, 1):
print('ChongChong')
else:
print('GomGom')'알고리즘 > 백준 문제 풀이' 카테고리의 다른 글
| [Python] 13249번 공의 충돌 (0) | 2023.09.02 |
|---|---|
| [Python] 18689번 Baklawa (0) | 2023.09.01 |
| [Python] 6068번 시간 관리하기 / 1263번 시간 관리 / 7983번 내일 할거야 (0) | 2023.08.30 |
| [Python] 13255번 동전 뒤집기 (4) | 2023.08.24 |
| [Python] 12046번 Not So Random (Small) / 12047번 Not So Random (Large) (0) | 2023.08.23 |

