최근 히스토그램에서 가장 큰 직사각형 문제에 대해 배우게 되어 다양한 풀이 방법을 작성해보고자 한다.
히스토그램에서 가장 큰 직사각형 문제란?
- 단위 길이의 폭을 가지는 막대들이 일렬로 나열된 히스토그램이 주어짐.
- 해당 히스토그램 내부에 포함되면서 가장 넓이가 넓은 직사각형을 구하는 문제이다.

막대들은 모두 단위 길이를 가지고 있기 때문에, 편의 상 막대의 높이들은 $A[i]$와 같은 형태의 배열로 주어진다고 하자.
즉, $A[i]$는 $i$번째 막대의 높이가 되는 것이다.
이 문제에서 가장 쉽게 생각할 수 있는 솔루션은 $\mathcal{O}(N^3)$짜리의 솔루션이다.
히스토그램에 포함되는 모든 직사각형을 조사하는 방법으로, 두 인덱스 $i, j$를 선택하고, 그 사이에 있는 모든 막대를 조사함으로써 막대 높이의 최솟값을 찾는다.
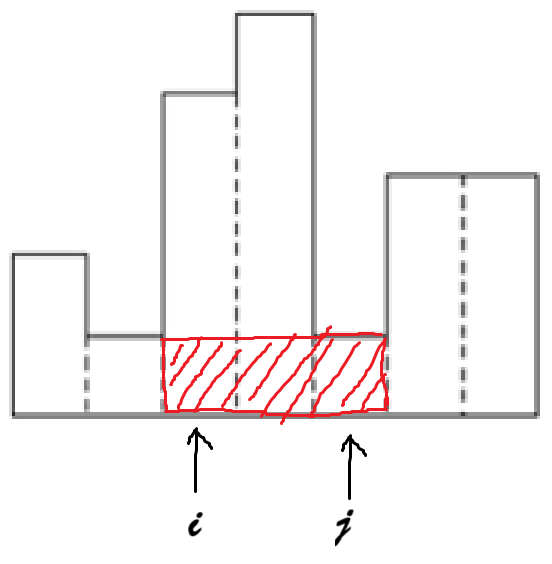
이때, $i$번째 막대에서 시작해서 $j$번째 막대로 끝나는 가장 큰 직사각형의 넓이는 $(j-i+1)\cdot \min(A[k]) \text{ where }(i \leq k \leq j)$가 된다.
두 인덱스를 선택하고, 그 사이의 최솟값을 찾는 방식이므로 $\mathcal{O}(N^3)$의 시간 복잡도가 소요된다.
파이썬 코드로 보면 다음과 같다.
'''
접근 방법:
O(N^3)의 시간 복잡도
나이브하게 인덱스 두개 i, j를 뽑고, A[i]~A[j]중 가장 작은 높이를 찾습니다.
시작이 i고 끝이 j인 직사각형의 넓이는 (j-i+1)*min(A[i]~A[j])가 됩니다.
따라서, 이를 그대로 구현하고 모든 직사각형의 넓이를 구한 다음 최댓값을 구해봅시다.
'''
N = int(input())
A = list(int(input()) for _ in range(N))
answer = 0
for i in range(N):
for j in range(i, N):
area = (j-i+1)*min(A[k] for k in range(i, j+1))
answer = max(area, answer)
print(answer)$\mathcal{O}(N^3)$솔루션을 조금 개선시키면 $\mathcal{O}(N^2)$솔루션을 낼 수 있다.
$\mathcal{O}(N^3)$ 방법을 보면, 구간 $[i, j]$와 $[i, j+1]$이 있을 때 중복되는 구간이 $[i, j]$임에도 불구하고 각 구간의 최솟값을 찾기 위해 불필요하게 순회를 더 하게 된다.
실제로는 $[i, j+1]$구간의 최솟값을 구하고자 할 때 $[i, j]$구간의 최솟값과 $j+1$번째 원소를 비교하기만 하면 충분하다.
즉, 실제로는 인덱스 $j$를 늘려가며 순회할 때 굳이 다시 $i$부터 $j$사이를 순회할 필요가 없다.
따라서, 투 포인터 기법처럼 $i$를 고정시킨 상태에서 $j$를 오른쪽으로 점점 늘려가며 넓이를 갱신시키면 된다.
파이썬 코드로 보면 다음과 같다.
'''
접근 방법:
O(N^2)의 시간 복잡도
두 개를 뽑고 그 사이를 본다면, 이미 봤던걸 보는 것이다.
최솟값을 구한다고 하면 굳이 그럴 이유가 없다!
하나를 뽑고, 남은 하나를 투포인터처럼 오른쪽으로 계속 늘려가며 최솟값을 갱신할 수 있다.
'''
N = int(input())
A = list(int(input()) for _ in range(N))
answer = 0
for i in range(N):
area, min_val = A[i], A[i]
for j in range(i, N):
min_val = min(min_val, A[j])
area = max(area, (j-i+1)*min_val)
answer = max(area, answer)
print(answer)놀랍게도 위의 풀이보다 시간 복잡도가 더 개선된 $\mathcal{O}(N\log N)$ 풀이가 존재한다.
크게 세그먼트 트리라는 자료구조를 사용한 풀이와 그렇지 않은 풀이로 나눌 수 있으나, 두 풀이 모두 분할 정복에 기반을 두고 있다.
따라서 세그먼트 트리를 사용하지 않은 풀이를 소개하도록 하겠다.
큰 틀은 다음과 같다.

히스토그램을 절반으로 쪼개면, 가장 큰 직사각형은 3가지의 경우 중 하나에 무조건 포함된다.(2가지가 아님에 유의하자.)
1. 왼쪽 부분 히스토그램에만 존재하는 경우
2. 오른쪽 부분 히스토그램에만 존재하는 경우
3. 두 부분 히스토그램 사이에 걸쳐있는 경우
1번과 2번의 경우 재귀 호출을 통해 쉽게 구할 수 있지만 3번의 경우가 조금 애매하다고 생각할 수 있다.
두 부분 히스토그램 사이에 걸쳐있다는 뜻은, 왼쪽 부분 히스토그램 끝 막대의 인덱스를 $mid$라고 할 때 $mid$를 항상 포함하며 오른쪽과 왼쪽으로 뻗어나가는, 가장 큰 직사각형을 의미한다.
위의 히스토그램의 경우 다음과 같은 그림으로 그려질 것이다.

투 포인터처럼 구하는 방법은 다음과 같다.
$A[mid]$를 초기 넓이로 삼고, $left = mid-1, right = mid+1$로 두 포인터를 선언한다.
이후 $mid$의 왼쪽 원소와 오른쪽 원소를 비교하고, 둘 중 큰 쪽으로 포인터를 늘려서 넓이를 갱신해준다.
포인터를 늘려서 넓이를 갱신하는 과정은 $\mathcal{O}(N^2)$에서 했던 방법과 같이, 이전 범위의 최솟값과 현재 원소를 비교하여 최솟값을 갱신하고, 이를 이용해 넓이를 갱신하면 된다.
이 과정을 모든 포인터가 범위를 벗어날 때까지 반복하면 된다. (만약 한쪽 포인터가 범위를 이미 벗어났다면, 남은 포인터만 계속 늘려서 넓이를 갱신시켜주면 된다.)
이를 통해 3가지 경우에 대한 최댓값을 반환하면 된다.
구간의 길이는 호출마다 절반씩 줄어들기 때문에, 재귀함수의 호출 깊이는 많아봤자 $\log N$번이 된다.
또한 해당 호출마다 사이에 걸쳐있는 최대 직사각형을 $\mathcal{O}(N)$의 시간복잡도로 구하기 때문에, 최종적으로 $\mathcal{O}(N \log N)$의 시간 복잡도를 가지게 된다.
이를 파이썬 코드로 보면 다음과 같다.
'''
접근 방법:
O(NlogN)의 시간 복잡도
이제 분할 정복 기법을 사용해봅시다.
임의의 히스토그램을 절반으로 나눴을 때, 다음과 같은 내용이 "항상" 성립합니다.
최대 넓이를 가진 직사각형은
1. 왼쪽에만 있는 경우
2. 오른쪽에만 있는 경우
3. 왼쪽과 오른쪽 사이에 걸쳐있는 경우
에만 존재한다.
1번과 2번은 재귀함수를 통해 똑같이 구하면 됩니다.
3번이 조금 거시기 한데, 3번은 경계에 걸쳐있는 막대를 mid라고하면,
mid에서 왼쪽, 오른쪽으로 투 포인터마냥 뻗어나가면서 O(N)만에 계산할 수 있습니다.
투 포인터로 뻗어나가며 구하는 방법은 다음과 같습니다.
현재 왼쪽 히스토그램의 경계에 있는 막대의 인덱스를 mid라고 하면,
left, right의 인덱스를 각각 mid-1, mid+1로 잡습니다.
left와 right를 비교해서 한쪽 막대가 더 크다면 그 쪽으로 늘리고 늘렸을 때의 넓이를 구해서 갱신합니다.
늘렸을 때의 넓이는 now_min*(right-left)가 됩니다.
구간의 길이는 호출마다 절반씩 감소하므로, 재귀함수 호출의 깊이는 많아봤자 logN번입니다.
따라서 총 시간 복잡도는 O(NlogN)이 됩니다.
'''
def divide_and_conquer(L, s, e):
if s > e: return 0
if s == e: return L[s]
m = (s+e)//2
left, right = divide_and_conquer(L, s, m), divide_and_conquer(L, m+1, e)
l, r = m, m
min_height = L[m]
mid = min_height*1
while True:
will_l, will_r = l-1, r+1
if will_l < s and will_r > e: break
if will_l < s:
min_height = min(min_height, L[will_r])
area = min_height*(will_r - l + 1)
mid = max(area, mid)
r = will_r
elif will_r > e:
min_height = min(min_height, L[will_l])
area = min_height*(r - will_l + 1)
mid = max(area, mid)
l = will_l
else:
if L[will_l] > L[will_r]:
min_height = min(min_height, L[will_l])
area = min_height*(r - will_l + 1)
mid = max(area, mid)
l = will_l
else:
min_height = min(min_height, L[will_r])
area = min_height*(will_r - l + 1)
mid = max(area, mid)
r = will_r
return max(left, right, mid)
N = int(input())
A = [int(input()) for _ in range(N)]
ans = divide_and_conquer(A, 0, N-1)
print(ans)
세그먼트 트리를 이용한 방법은 이와 유사한데, 절반으로 쪼개는 것이 아닌 구간의 최솟값을 기준으로 왼쪽, 오른쪽을 분리하고, 구간의 최솟값을 포함하는 가장 큰 직사각형(이는 구간의 길이와 구간의 최솟값을 곱한 값이다)을 비교하여 최댓값을 구한다.
+) 똑같은 시간 복잡도 $\mathcal{O}(N \log N)$을 지닌, 분리 집합을 활용한 풀이도 존재한다.
풀이 방법은 꽤나 직관적이다.
먼저, 가장 높은 막대(만약, 막대가 여러 개라면 그 중 가장 작은 인덱스를 가진 막대)부터 시작해서, 낮은 막대 순으로 자기 자신과 인접한 막대들을 모두 유니온 해준다.
해당 분리 집합 연산을 통해 해당 막대가 붙어있는 덩어리의 크기를 구할 수 있으며, 그 덩어리의 크기와 해당 막대의 높이를 곱하면 해당 막대가 포함된 가장 큰 직사각형의 넓이를 구할 수 있다.
그 넓이를 통해 계속해서 답을 갱신해나가면 된다.
그림으로 표현하자면 아래와 같다.


이 과정 속에서 나타난 주황색, 초록색, 노랑색 사각형의 넓이들 중 최댓값을 구하면 그것이 답이 될 것이다.
정렬 과정에서 $\mathcal{O}(N\log N)$의 시간 복잡도가 소요되고, 유니온 파인드를 하는 과정에서 $\mathcal{O}(N\alpha(N))$의 시간 복잡도가 소요되므로, $\mathcal{O}(N\log N)$의 시간 복잡도를 가지게 된다.
구현할 때 주의할 점은 유니온 파인드를 사용하기 때문에, Path compression + Union by size/rank를 사용해주어야 해당 시간 복잡도가 나올 수 있다는 점이다.
이를 파이썬 코드로 보면 다음과 같다.
'''
접근 방법:
가장 높이가 높은 막대에서 낮은 막대 순으로 인덱스 리스트를 정렬합시다.
이후 해당 인덱스 리스트 순으로 유니온 파인드를 진행해줍니다.
유니온 파인드를 할 때엔 당연히 자신의 왼쪽과 오른쪽이 연결되있는지 확인하고 유니온 파인드를 진행합니다.
유니온 파인드를 진행한 후에는 해당 막대의 길이*집합의 크기가 해당 막대가 포함된 넓이의 최댓값이 되고,
이 넓이를 답에 갱신해주면서 답을 구해주면 됩니다.
'''
import sys
input = sys.stdin.readline
N = int(input())
A = list(int(input()) for _ in range(N))
idx_li = sorted(range(N), key=lambda x: (-A[x], x))
parent = [-1 for _ in range(N)]
size = [0 for _ in range(N)]
def find(node):
if parent[node] != node:
parent[node] = find(parent[node])
return parent[node]
def union(node1, node2):
p1, p2 = find(node1), find(node2)
if p1 == p2:
return
if size[p1] < size[p2]:
p1, p2 = p2, p1
parent[p2] = p1
size[p1] += size[p2]
ans = 0
for node in idx_li:
parent[node] = node
size[node] = 1
if node + 1 < N:
if parent[node+1] != -1:
union(node, node+1)
if node - 1 >= 0:
if parent[node-1] != -1:
union(node, node-1)
area = A[node]*size[find(node)]
ans = max(area, ans)
print(ans)가장 최적화 된 풀이의 시간 복잡도는 $\mathcal{O}(N)$이다.
이는 단조증가하는 스택의 성질을 이용한 풀이로, 특정 조건에 따라 스택에 막대를 넣었다 빼면서 최대 직사각형의 넓이를 구하는 방법이다.
풀이를 설명하기에 앞서, 다음 영상을 보자.
https://www.youtube.com/watch?v=lktr76SxB2w
넓이가 최대인 직사각형이 어디에 있는지는 잘 모르지만, 확실한 정보는 넓이가 최대인 직사각형은 항상 어떤 막대를 온전히 포함하고 있다는 사실이다.
따라서, $i$번째 막대를 온전하게 포함하면서 가장 큰 직사각형의 넓이를 모든 $i$마다 구해주면 된다.
그렇다면 이걸 빠르게 구하는 것이 관건일 것이다.
$i$번째 막대의 오른쪽에 있으면서 $i$번째 막대보다 처음으로 작게 되는 위치를 $right[i]$라고 하고, $i$번째 막대의 왼쪽에 있으면서 $i$번째 막대보다 처음으로 작게되는 위치를 $left[i]$라고 한다면, $i$번째 막대를 포함하면서 가장 큰 직사각형의 넓이는 $(right[i] - left[i] - 1)\cdot A[i]$가 된다.

따라서, 이 과정을 모든 $i$에 대해 빠르게 수행해주면 된다. 그리고 이는 단조증가하는 스택(Monotone Stack)을 사용하여 쉽게 구현할 수 있다.
다음과 같은 과정을 따른다.
먼저, 원소를 하나씩 보면서 스택에 넣는데, 이때 스택이 항상 오름차순으로 정렬되도록 스택에 원소를 넣는다. 구체적으로 이야기하자면, 다음과 같이 스택에 원소를 넣는다.
1. 스택이 비어있다면 스택에 원소를 넣는다.
2. 그렇지 않다면, 현재 보고있는 원소와 스택의 가장 위 원소를 비교한다. 만약 스택의 가장 위 원소가 현재 원소보다 크거나 같을 경우 스택의 가장 위 원소를 뺀다.
3. 2번이 성립하지 않을 때까지 원소를 뺀다. 이후 스택에 현재 원소를 집어넣는다.
이 과정을 반복하면 모든 순간마다 스택의 원소가 오름차순으로 정렬된다.
2번 과정을 보면, 스택의 가장 위 원소가 현재 원소보다 크거나 같다면, 즉, 현재 원소가 스택의 가장 위 원소보다 작다는 말이므로 스택의 가장 위 원소보다 오른쪽에 있으면서 처음으로 작아지는 지점을 찾을 수 있다.
즉, 스택의 가장 위 원소의 인덱스를 $top \ idx$라고 한다면, $right[top \ idx] = i$에 해당하는 것을 확인할 수 있다.
스택은 항상 단조증가하도록 "정렬"되어 있으므로, 스택의 두번째 위 원소는 항상 $A[top \ idx]$보다 작으며, 스택의 두번째 위 원소의 인덱스가 곧 $left[top \ idx]$에 해당함을 확인할 수 있다.
사실 스택에 넣고 뺄 때 인덱스만 저장해도 대소관계를 따질 수 있으므로 스택에 넣고 빼는 원소들은 모두 인덱스라고 생각해보자.
스택에서 원소(인덱스)를 뺀 후, 뺀 인덱스를 $top \ idx$라고 한다면 $A[top \ idx] \cdot (i - stack[-1] - 1)$이 $top \ idx$번째 막대를 포함하는 가장 큰 직사각형의 넓이가 될 것이다.
만약 스택에서 원소(인덱스)를 뺐는데 더 이상 스택에 원소가 존재하지 않는다면, $left[top \ idx] = -1$이라고 간주할 수 있으므로 $A[top \ idx] \cdot i$가 직사각형의 넓이가 될 것이다.
그렇게 스택을 사용하여 모든 원소를 넣었다 뺐다를 반복하면 스택에 남은 원소들이 존재하게 되는데, 해당 남은 원소들의 $right[top \ idx]$는 모두 $N$이라고 간주할 수 있고, 이를 통하여 스택에 더 이상 남은 원소가 존재하지 않을 때 까지 원소를 빼며 넓이를 갱신해 줄 수 있다.
해당 알고리즘을 파이썬 코드로 구현하면 다음과 같다.
# 1725번 히스토그램
# 히스토그램에서 가장 큰 직사각형 문제
'''
접근 방법:
O(N)의 시간 복잡도
히스토그램 문제에서 찾을 수 있는 최적의 시간 복잡도입니다.
다음과 같은 아이디어를 생각해봅시다.
넓이가 최대인 직사각형은 어디엔가 존재합니다.
그리고 이 직사각형은 반드시 어디엔가 i번째 막대를 "온전하게" 포함하고 있을 것입니다.
https://www.youtube.com/watch?v=lktr76SxB2w
0
00 0
00 0 0
0000 0
000000
000000
예를 들어 3번째 막대를 봅시다.
right[i] = i번째 막대 오른쪽에 있는 h[i]보다 작은 막대의 첫 위치
left[i] = i번째 막대 왼쪽에 있는 h[i]보다 작은 막대의 첫 위치
height[i] = i번째 막대의 높이
라고 정의한다면,
i번째 막대를 항상 포함하는 가장 큰 직사각형의 넓이는 다음과 같습니다.
height[i]*(right[i]-left[i]-1)
이를 모든 i에 대해 빠르게 수행하면 구할 수 있습니다.
이 작업은 증가하는 스택을 사용하면 쉽게 구할 수 있습니다.
다음과 같은 방법으로 증가하는 스택을 만듭시다.
1. 원소를 왼쪽부터 오른쪽 순으로 봅니다.
2. 만약 현재 스택이 비어있거나, 현재 스택의 가장 위 원소보다 현재 보고있는 원소가 클 경우, 해당 원소를 스택에 넣어줍니다.
현재 스택의 가장 위 원소는 현재 보고있는 원소 왼쪽에 있는 h[i]보다 작은 막대의 첫 위치가 됩니다.
3. 만약 현재 스택의 가장 위 원소보다 현재 보고있는 원소가 작거나 같을 경우,
현재 스택의 가장 위 원소보다 현재 원소가 작을 때 까지 현재 스택을 pop해줍니다.
이때, 현재 스택의 가장 위 원소의 오른쪽에 있는, h[i]보다 작은 막대의 첫 위치는 현재 원소가 됩니다.
이를 이용하여 구해봅시다.
'''
N = int(input())
A = list(int(input()) for _ in range(N))
stack = [] # 스택에는 인덱스를 저장합시다.
ans = 0 # 넓이를 갱신하도록 ans라고 저장합시다.
for i in range(N):
ele = A[i]
# 스택이 비어있거나 스택의 최상단 원소(인덱스)가 가르키는 원소가 현재 원소보다 작다면 종료
while stack and A[stack[-1]] >= ele:
top_idx = stack.pop()
if stack == []:
area = A[top_idx]*(i)
else:
area = A[top_idx]*(i-stack[-1]-1)
ans = max(ans, area)
stack.append(i)
while stack:
top_idx = stack.pop()
if stack == []:
area = A[top_idx]*(N)
else:
area = A[top_idx]*(N-stack[-1]-1)
ans = max(ans, area)
print(ans)이 문제와 관련된 문제를 소개하겠다.
'알고리즘 > 알고리즘' 카테고리의 다른 글
| 보이어-무어 다수결 투표 알고리즘(Boyer-Moore Majority Vote Algorithm) (0) | 2022.09.09 |
|---|---|
| CCW 알고리즘(CCW Algorithm) (1) | 2022.08.26 |

