보이어-무어 다수결 투표 알고리즘(Boyer-Moore Majority Vote Algorithm)

최근에 배우게 된 보이어-무어 다수결 투표 알고리즘에 대해 글을 써보고자 한다.

 

---

보이어-무어 다수결 투표 알고리즘이란?

 

• K명의 후보들이 N명에게 투표받을 때, 과반수 이상인 후보가 나오는지, 나온다면 그 후보가 어떤 후보인지 알아내는 알고리즘.
• 과반수 후보를 가려내는 방법 중 브루트 포스를 이용한 방법과 맵을 이용한 방법(파이썬에서는 딕셔너리 자료형)보다 시간복잡도, 공간 복잡도 면에서 우월함.
• O(N)의 시간 복잡도로 판단 가능함. 반면, 브루트 포스를 이용한 방법은 O(N^2) 임. 맵을 이용한 방법은 같은 시간 복잡도를 차지하나, 메모리를 더 많이 차지함.
• 스트리밍 알고리즘의 대표적인 예시임.(공간복잡도가 O(1) 임)

---

 

이 알고리즘은 두 부분으로 이루어져 있다.

 

첫 부분은 과반수 원소가 될 수 있는 후보를 골라내는 부분, 두 번째 부분은 그 후보가 실제로 과반수 원소인지 확인하는 부분이다.

 

처음에 과반수 원소가 될 수 있는 후보를 저장하는 major라는 변수와 이 major라는 변수가 실질적으로 몇 번 등장했는가를 알려주는 count라는 변수가 필요하다.(변수 두 가지만 있어도 가능)

 

그리고 배열을 for문으로 순회하면서 배열의 원소가 major와 같으면 count 변수를 +1 해준다.

 

그렇지 않다면 count 변수를 -1을 해준다.

 

count 변수가 0이 되는 경우는 major변수가 지금까지 실질적으로 0번 등장한 것과 다름이 없으므로, 이때는 major라는 변수를 현재 순회하고 있는 배열의 원소로 교체해준다.(다시 말하자면, 후보 교체)

 

이 첫 번째 부분을 파이썬 코드로 옮긴 코드는 다음과 같다.

---

def boyer_moore_majority(arr):
    count = 0 # 과반수 원소 후보가 실질적으로 몇개 있는가?
    major = 0 # 과반수 원소 후보의 번호
    for ele in arr:
        if count == 0:  # 후보가 실질적으로 0번 등장했다면
            major = ele  # 후보 교체
        if major == ele:  # 후보가 등장하면
            count += 1 
        else:
            count -= 1

---

 

이 첫 부분에 대한 증명을 간략하게 하자면 다음과 같다.

 

첫 부분을 거치면, major라는 변수에는 과반수의 후보가 될 수 있는 원소가 담길 것이다.

 

여기서 "후보"라고 말한 이유는 이 원소가 실제로 과반수가 아닐 수도 있기 때문이다.

 

하지만, 이 major 변수에 담긴 원소 외의 다른 원소는 절대로 과반수가 될 수 없다.

 

곰곰이 생각해보면 당연한 사실이기 때문에, 귀류법을 사용하여 이 사실을 증명해보고자 한다.

증명)

major 변수에 담긴 원소 외의 배열의 다른 원소가 과반수 원소가 될 수 있다고 가정하자.

편의를 위해 major 변수에 담긴 원소를 1번 원소, 과반수 원소인 배열의 다른 원소를 2번 원소라고 하자.

배열의 길이를 K라고 가정한다면, 2번 원소는 (K//2+1) 번 이상 배열에 등장할 것이다.
(2번 원소가 과반수 원소이기 때문에)

그렇다면 1번 원소는 아무리 많아봤자 (K//2-1) 번 등장한다.
(물론 또 다른 원소가 있다면 이것보다 더 적을 수도 있다.)

위에 코드에 따르면, 1번 원소가 등장하는 횟수보다 2번 원소가 등장하는 횟수가 더 많기 때문에 count 변수는 중간에 0을 한번 거칠 수밖에 없으며, 그렇다면 major라는 변수 또한 2번 원소로 교체된다.

이는 major변수가 1번 원소라는 가정에 모순이다.

 

이 증명 과정을 간단하게 비유하자면 다음과 같다.

 

전쟁을 하는데 성 하나를 두고 차지하는 싸움을 한다고 해보자.

 

병사들이 한 명씩 나오는데 성이 비어있는 경우 병사가 그 성으로 들어간다.

 

같은 편을 만나면 성에 합류하고, 다른 편을 만나면 성을 차지하고 있는 병사 한 명이 나가서 그 다른 편과 나가서 싸우다가 같이 죽는다.

 

여기서 성은 major변수에 해당된다. 그리고 성 안에 들어가 있는 병사가 몇 명인지는 count변수에 해당이 된다.

---

보이어-무어 알고리즘을 간략하게 표현하는 그림.

---

더 쉬운 이해를 돕기 위해 다음 그림을 가져와보았다.

 

총 16개의 표가 주어져 있고, 이 표들이 ●, ★, ■로 갔다고 해보자.

 

for문을 돌면서 배열의 원소를 확인하는데, 현재 major변수와 같은 원소가 나오면 +1, 아니면 -1을 해주다가 0이 되면 major 변수를 현재 원소로 새롭게 교체하는 방식이다.

 

---

 

하지만 위의 그림을 조금 변형해 아래 그림과 같이 있다고 가정해보자.

---

배열의 원소가 10개 있을 때

---

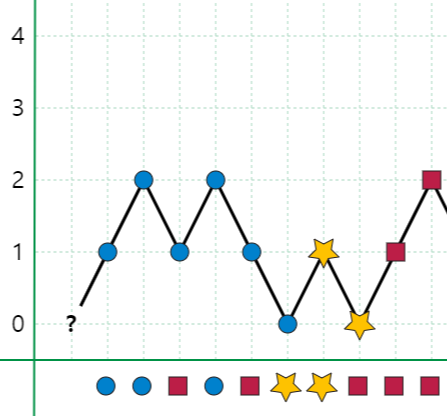
배열의 원소가 10개밖에 없다고 가정해보자.

 

분명 이 그림에서 나온 것과 같이, 과반수인 원소는 존재하지 않는다. 하지만 major 변수에 담겨있는 원소는 현재 ■이고, count변수는 2로 되어있다.

 

이렇듯, 앞서 언급했듯이 major라는 변수는 언제까지나 과반수 원소가 될 수 있는 "후보"에 불과할 뿐이지, 실제로 과반수 원소인 것은 아니다.

 

때문에, 실제로 이 원소가 과반수 원소 인지를 체크해주는 부분이 필요하다.

 

여기에선 major변수가 몇 번 등장했는지 확인하는 m이라는 변수가 필요하다.

 

배열의 원소들을 for문으로 확인하면서 배열의 원소가 major과 같으면 m에 +1을 해준다.

 

이후, m이 배열의 길이의 절반보다 큰지 확인하면 된다.

 

앞서 언급한 첫 번째 부분과 합쳐서 작성한 최종 파이썬 코드는 다음과 같다.

 

---

 def boyer_moore_majority(arr):
    count = 0 # 과반수 원소 후보가 실질적으로 몇개 있는가?
    major = 0 # 과반수 원소 후보의 번호
    for ele in arr:
        if count == 0:  # 후보가 실질적으로 0번 등장했다면
            major = ele  # 후보 교체
        if major == ele:  # 후보가 등장하면
            count += 1 
        else:
            count -= 1
    k = len(arr)
    m = 0  # 정말 과반수 인지 체크용 변수
    for ele in arr:  # 정말 과반수가 맞는지 확인
        if ele == major:
            m += 1
    if m > k//2:
        return m, major # 과반수 원소가 몇개 있는지와 그 원소 반환
    else:
        return None, None

---

이 알고리즘을 활용하여 풀 수 있는 대표적인 문제를 소개하겠다.

 

1270번: 전쟁 - 땅따먹기 (acmicpc.net)

1270번: 전쟁 - 땅따먹기

그냥 이 알고리즘을 그대로 구현하는 문제라고 볼 수 있는 아주 기초적인 문제이다.

 

물론, 맵을 사용한 방법으로 문제를 풀 수도 있겠지만, 그 방법보다 이 알고리즘이 메모리와 시간 또한 적게 든다는 것을 확인할 수 있을 것이다.

 

참고 자료:
1. Boyer–Moore majority vote algorithm - Wikipedia
2. Boyer-Moore 과반수 투표 알고리즘 - Sungho's Blog (sgc109.github.io)
3. 스트리밍 알고리즘 - 위키백과 (wikipedia.org)
4. Find majority element (Boyer–Moore Majority Vote Algorithm) (techiedelight.com)
5. 동적, 스트리밍, 온라인 알고리즘 비교 (Dynamic, Streaming, and Online Algorithm) (tistory.com)

 

---

+) 다음 영상도 참고해보면 좋을 것이다.

https://youtu.be/DTWLKMwolAY?si=1DffPATJi2AwNYRu