최근에 배우게 된 CCW 알고리즘에 대해 글을 써보고자 한다.
CCW 알고리즘이란?
- Counter-ClockWise의 줄임말로, 직역하면 반시계 방향이라는 뜻임.
- 세 점 p1, p2, p3가 주어져 있고, 이 세 점을 p1, p2, p3 순서대로 직선으로 이었을 때, 시계방향으로 휘어지는가, 반시계 방향으로 휘어지는가, 혹은 일직선을 이루는가를 판별하는 알고리즘.
- 방향이 중요하기 때문에 벡터의 개념을 알아야 함.
- 이 알고리즘을 활용하여 다양한 기하학 알고리즘에 적용할 수 있음. 대표적으로 선분 교차 판정 알고리즘, 볼록 껍질 알고리즘(컨벡스 헐) 등이 있음.
요약된 내용으로만 보아서는 무슨 뜻인지 잘 모를 수도 있을 것이다.
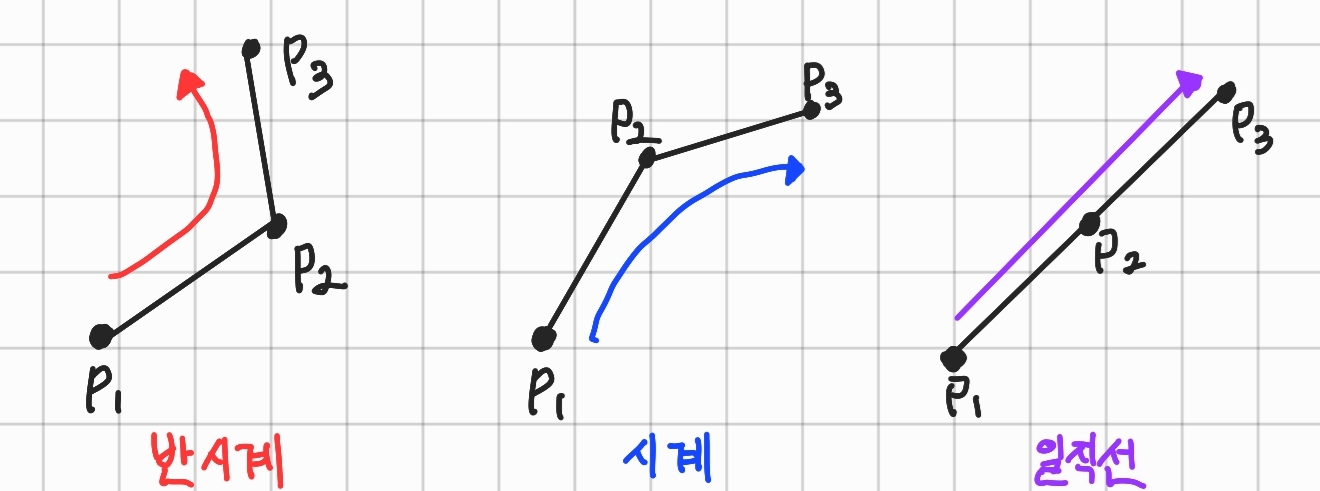
그래서 다음과 같이 그림을 준비했다.
위의 그림처럼 세 점 P1, P2, P3를 순서대로 이을 때, 시계 방향으로 휘어져 있는지 반시계 방향으로 휘어져 있는지 일직선인지를 판단하는 알고리즘이 CCW 알고리즘이다.
때문에, 같은 점이 놓여있더라고 할 지라도, CCW 알고리즘에서는 순서가 중요하다.
만약, 위의 그림의 왼쪽 부분과 같이 P1 -> P2 -> P3 순으로 이은 선을 CCW 알고리즘으로 방향을 판단한다면 반시계 방향이 나올 것이다.
하지만, 왼쪽 부분을 P3 -> P2 -> P1 순으로 이은 선을 CCW 알고리즘으로 방향을 판단하면 시계 방향이 나올 것이다.
또한, CCW 알고리즘은 방향이 중요하기 때문에, 아래 그림과 같이 벡터의 개념이 활용이 된다.

먼저, 첫 번째 그림의 왼쪽 부분과 같은 상황을 가져와서 그려보았다.
선을 그을 때, 우리는 P1에서 P2로 잇는 선을 그은 후, P2에서 P3로 선을 긋는다.
이렇게 P1에서 P2로 향하는 벡터를 a라고 하고, P2에서 P3로 향하는 벡터를 b라고 하자.
이제 우리는 두 벡터가 시계 방향으로 회전하는지, 반시계 방향으로 회전하는지, 일직선을 이루는지 외적 연산(cross product)을 통하여 확인할 것이다.
외적 연산은 아래 그림과 같은 특징을 가지고 있다.

a×b를 계산한 결과는 다음과 같이 벡터로 나오게 되는데, 그 방향과 크기는 a와 b가 놓여진 면의 수직 한 방향이며, 그 크기는 |a||b|sin(a와 b가 벌어진 각)과 같다.
외적을 계산할 때는 위의 그림과 같이 a에서 b로 회전하는 방향을 오른손의 네 손가락으로 감 싸돌듯 표현하며 계산하는데, 이때 엄지 손가락이 향하는 방향이 외적의 결괏값 방향이다.
이 오른손의 네 손가락이 감싸도는 방향은 항상 반시계 방향이므로, 만약 우리가 a×b를 계산할 때, a와 b가 순서대로 반시계 방향을 이루고 있다면 외적의 결과값은 윗 방향을 향하게 될 것이다.
반대로, a와 b가 순서대로 시계 방향을 이루고 있다면 아래 그림과 같이 외적의 결괏값은 아랫 방향을 향하게 될 것이다.

외적은 3차원에서 정의되는 연산이기 때문에, 평면벡터 a와 b에 외적을 적용할 때에는 a의 z성분과 b의 z성분이 모두 0이라고 생각하고 외적을 적용하면 된다.
외적의 결과값은 행렬식으로 다음과 같이 표현하여 계산을 하게 되는데, 우리는 두 벡터 a와 b가 모두 xy평면 위에 있다는 것을 잘 안다.

그래서 외적의 결괏값을 계산하면 axby - aybx부분만 남게 되는데, 만약 이 부분이 양수라면 외적의 방향이 위쪽 방향을 향하고 있는 것이고, 곧 a에서 b로 가는 회전방향이 시계 반대 방향을 이루고 있다는 뜻이 된다.
만약 이 부분이 음수라면 외적의 방향이 아랫 방향을 향하고 있다는 뜻이고, 곧 a에서 b로 가는 회전 방향이 시계 방향을 이루고 있다는 뜻이 된다.
다시 맨 위의 그림 상황으로 되돌아 가보자.

점 P1 -> P2 -> P3 순서대로 이은 선은 시계 방향을 이루고 있을까? 시계 반대 방향을 이루고 있을까?
벡터 P1P2와 벡터 P2P3를 각각 벡터 a, 벡터 b라고 하자.
위에서 이야기한 것처럼, 이 벡터 a와 벡터 b를 외적 한 값이 양수라면 벡터 a에서 벡터 b로 회전하는 방향이 시계 반대 방향을 이루고 있다고 했다.
벡터 a에서 벡터 b로 회전하는 방향이 서로 시계 반대 방향을 이룬다면 두 벡터의 시작점과 끝점을 이었을 때, 선이 휘어지는 방향 또한 시계 반대 방향이라는 것을 우리는 그림을 통해 쉽게 알 수 있다.
다시 말해, 벡터 a와 벡터 b를 그냥 외적 해서, 양수가 나오면 시계 반대 방향, 음수가 나오면 시계 방향, 0이 나오면 아무것도 아니므로 일직선이라고 판단할 수 있는 것이다!
요약하자면 다음과 같다.
P1 -> P2 -> P3 순으로 이은 선이 시계 방향으로 휘어있는지 반시계 방향으로 휘어있는지, 일직선을 이루는지 판단하고 싶을 때, 다음과 같이 판단한다.
| 1. 벡터 P1P2와 벡터 P2P3를 각각 벡터 a와 벡터 b라고 정한다. (어떻게 보면 P1, P2, P3도 벡터라고 간주할 수 있으므로, 이 벡터들을 따로 방향벡터(direction vector)라고 부르자.) |
| 2. 방향 벡터 a와 b를 위에 나온 외적 식을 통해 외적 값을 계산해준다. |
| 3. 그 결과 값이 양수라면 반시계, 음수면 시계, 0이라면 일직선을 이루고 있는것임. |
이를 이용한 의사 코드(Pseudocode)는 다음과 같다.
def direction_vector(point1, point2): # 점 P1에서 P2로 가는 방향벡터 생성
return (point2_x - point1_x, point2_y - point1_y)
def cross_product(vector_a, vector_b): # 평면 벡터 a와 평면 벡터 b를 외적한 값을 반환하는 함수
return vector_a_x*vector_b_y - vector_a_y*vector_b_x
def CCW(P1, P2, P3): # P1->P2->P3 순으로 이었을 때 반시계방향이면 1, 시계방향이면 -1, 일직선이면 0
vector_a = direction_vector(P1, P2)
vector_b = direction_vector(P2, P3)
k = cross_product(vector_a, vector_b)
if k > 0: # 양수면 반시계 방향
return 1
elif k < 0: # 음수면 시계 방향
return -1
else: # 그 외의 경우는 일직선
return 0그러면 이를 이용하여 풀 수 있는 대표적인 문제를 소개하겠다.
https://www.acmicpc.net/problem/11758
11758번: CCW
첫째 줄에 P1의 (x1, y1), 둘째 줄에 P2의 (x2, y2), 셋째 줄에 P3의 (x3, y3)가 주어진다. (-10,000 ≤ x1, y1, x2, y2, x3, y3 ≤ 10,000) 모든 좌표는 정수이다. P1, P2, P3의 좌표는 서로 다르다.
www.acmicpc.net
말 그대로 위에서 설명했던 CCW함수를 그대로 구현하기만 하면 되는 CCW 알고리즘 기초 중 기초 문제이다.
CCW 알고리즘은 다른 기하 알고리즘의 기초가 된다.
이를 이용하여 다각형의 넓이, 선분 교차 판정, 볼록 껍질 알고리즘 등을 배울 수 있다. 이에 대한 내용들은 다음 글에서 서술할 예정이다.
'알고리즘 > 알고리즘' 카테고리의 다른 글
| 보이어-무어 다수결 투표 알고리즘(Boyer-Moore Majority Vote Algorithm) (0) | 2022.09.09 |
|---|
