대수학 시리즈의 첫 글입니다.
먼저, 이 글은 John B. Fraleigh의 A First Course in Abstract Algebra를 참고자료로 하여 쓰였음을 밝힙니다.
이 섹션에서는 수학이라는 언어의 "기본"이라고 말할 수 있는 "집합"에 대해 간략하게 설명한 후, "같다"라는 개념을 어떻게 수학에서는 이야기 하고 있는가에 대해 이야기합니다.
이 섹션의 주요한 내용을 꼽자면, 동치관계(Equvalence Relation)와 집합의 분할(Partition)입니다.
이를 이해해 보기 위해 글을 따라가 봅시다.
우리는 모든 것을 "완벽하게" 정의 내릴 수 없습니다. 당장 집합만 해도 그렇습니다. 예를 들어볼까요?
예를 들어, 집합을 "잘 정의된 것들의 모임"이라고 정의해 봅시다.
그러면, 자연스럽게 "모임"은 뭔데?라고 반문할 수 있고, "모임은 어떤 것들의 구성체"야,라고 정의를 내린다면, 누군가가 "구성체는 뭔데?라고 물어볼 수 있습니다.
인간이 사용하는 단어들은 그 개수가 제한되어 있기 때문에 필연적으로 순환적으로 이야기될 수 있는 부분이 존재할 수밖에 없습니다.
때문에 여기선 "집합"이 무엇인가에 대해서는 논하지 않습니다. 단지 "집합"이 어떠해야 된다,는 이야기할 것입니다.
우리가 집합에 대해 잘 알고 있는 것들을 이야기하자면 아래와 같습니다.
1. 집합은 원소로 구성되어 있으며, 원소 $a$가 집합 $S$에 들어가 있다면, 이를 $a \in S$로 표기합니다.
2. 원소가 존재하지 않는 집합은 하나뿐이며, 이를 공집합이라고 하고 $\varnothing$로 표기합니다.
3. 집합을 구성하고 있는 원소들의 특징을 $P(x)$라고 한다면, 우리는 집합을 $\{ x | P(x) \}$와 같이 표기할 수 있습니다.
4. 집합이 "잘 정의"(Well-defined)되어 있다는 뜻은, 어떤 집합을 정의한다면, 그 집합에 원소가 들어있거나 들어있지 않음을 의미합니다. 즉, 배중률이 잘 적용됨을 뜻합니다.
5. 집합 $S$에 있는 원소의 개수를 $S$의 Cardinality라고 하며, $|S|$로 표기합니다.
6. 집합 $A$가 집합 $B$의 부분집합이라는 말은, $A$의 모든 원소가 $B$에도 속함을 의미합니다. 이를 $A \subseteq B$로 표기합니다. 이때, $B$의 모든 원소가 $A$에도 속한다면, 즉, $A$와 $B$가 같다면 $A = B$로 표기합니다. 그렇지 않은 경우에는 $A \subset B$로 표기합니다.
7. 집합 $A$와 집합 $B$가 있을 때, 두 집합의 Cartesian Product는 아래와 같은 집합을 의미합니다.
$A \times B = \{(a, b) \ | \ a \in A \ and \ b \in B\}$
8. 정수 집합, 유리수 집합, 실수 집합을 각각 $\mathbb{Z}, \mathbb{Q}, \mathbb{R}$로 표기합니다.
각 집합별로 양수만 모은 집합은 각각 $\mathbb{Z}^{+}, \mathbb{Q}^{+}, \mathbb{R}^{+}$로 표기합니다.
각 집합별로 $0$을 제외한 집합은 각각 $\mathbb{Z}^{*}, \mathbb{Q}^{*}, \mathbb{R}^{*}$로 표기합니다.
9. 두 집합이 서로소(Disjoint)라는 말은, $A \cap B = \varnothing$을 의미합니다. 즉, 두 집합에 공통된 원소가 존재하지 않음을 의미합니다.
여기서 중요한 것은 Cartesian Product입니다. 두 집합 혹은 두 대상 사이의 "무언가"를 이야기할 때에는 빠지지 않는 개념이기 때문입니다.
Cartesian Product를 이용하여 다음과 같이 관계(Relation)를 정의합니다.
집합 $A$와 $B$사이의 Relation이란, $A \times B$의 부분집합 $\mathscr{R}$을 의미합니다.
$(a, b) \in \mathscr{R}$이라면, 우리는 $a$와 $b$가 관계(related)되어있다고 이야기 하며, 이를 $a \mathscr{R} b$와 같이 표기합니다.
신기한 점은, "관계되어 있다"는 말이 단순히 순서쌍 집합의 부분집합에 들어가 있냐 들어가 있지 않냐로 이야기된다는 점입니다.
순서쌍 집합의 부분 집합 안에 들어가 있다는 말이 도대체 "관계"를 왜 나타내는 것이냐? 에 대해 의문을 가지실 수도 있습니다.
대표적인 예시를 하나 들어봅시다. 우리는 $=$기호에 익숙합니다.
예를 들자면, $5 = 5$입니다. 당연하죠?
이 당연한 "관계"를 위에서 정의한 Relation을 통해 표현한다면 아래와 같이 표현할 수 있습니다.
-항등 관계(Equality Relation)
$=$은 집합 $S \times S$의 부분 집합 $\{ (x, x) \ | \ x \in S \}$을 의미합니다.
따라서, 모든 $x \in S$에 대해, $x = x$입니다. 즉, $(x, x) \in =$입니다.
당연한 이야기를 대수학에서는 이렇게 어렵게 표현합니다. 그 이유는 수학의 언어는 "집합"에 기반을 두고 있기 때문입니다.
앞서 이야기했듯, 두 대상이 있다면 그것을 Relation을 통해 이야기할 수 있다고 했습니다.
두 대상이 관련되는 아주 좋은 예시는 바로 "함수"입니다.
우리는 이제 함수를 Relation을 통해 정의할 것입니다.
집합 $X$에서 집합 $Y$로 대응되는 함수(Function) $\phi$는 다음과 같은 조건을 만족시키는 Relation입니다.
- 모든 $x \in X$는 정확히 하나씩 $\phi$의 원소, 즉, 순서쌍 $(x, y)$의 첫 번째 원소로 나타나야 합니다.
이때, 함수(Function)는 Map, 혹은 Mapping이라고 부르기도 합니다.
우리는 함수 $\phi$와 집합 $X$, $Y$를 묶어서 $\phi : X \rightarrow Y$와 같이 표기합니다.
또한, $(x, y) \in \phi$(Set Notation)를 $\phi (x) = y$(Function Notation)와 같이 표기합니다.
집합 $X$는 함수 $\phi$의 정의역(Domain)이라고 부르고, 집합 $Y$는 함수 $\phi$의 공역(Codomain)이라고 합니다. 또한, $\phi [X] = \{ \phi (x) \ | \ x \in X \}$을 함수 $\phi$의 치역(Range)이라고 합니다.
이렇듯 Relation으로 정의한 함수는, 기존에 우리가 가지고 있던 함수의 개념에 아주 잘 부합합니다.
한편, 우리가 알고 있던 덧셈, 뺄셈, 곱셈, 나눗셈과 같은 사칙 연산도 함수의 일종으로 바라볼 수 있습니다.
예를 들자면, 실수 집합 $\mathbb{R}$위에서의 덧셈 연산은 다음과 같은 함수의 일종으로 바라볼 수 있습니다.
$$ + : (\mathbb{R} \times \mathbb{R} ) \rightarrow \mathbb{R} $$
즉, $\mathbb{R} \times \mathbb{R}$에서 $\mathbb{R}$로 가는 함수입니다.
위에서 언급한 함수 표기법을 사용한다면, $(2, 3) \in \mathbb{R} \times \mathbb{R}$에 작용하는 덧셈 연산은 $+((2, 3)) = 5$과 같이 표기할 수 있습니다. 집합 표기법을 사용한다면, $((2, 3), 5) \in +$와 같이 표기할 수도 있습니다. 하지만, 우리가 일반적으로 익숙하게 느끼는 표기법은 $2+3=5$와 같은 표기법입니다.
연산과 관련된 이야기들은 뒤 섹션에서 좀 더 자세하게 다룰 예정입니다.
한편, 우리에게 익숙한 함수를 정의했으니 이와 관련된 개념들, 즉, 단사 함수(one-to-one), 전사 함수(onto), 일대일 대응(one-to-one correspondence), 역함수(inverse function)에 관한 이야기를 해봅시다.
- 단사, 전사, 일대일 대응, 역함수
함수 $\phi : X \rightarrow Y$가 $x_1 = x_2$일 때만 $\phi (x_1) = \phi (x_2)$라면, 이 함수 $\phi$를 단사 함수(one-to-one)라고 부릅니다.
또한, 함수 $\phi$의 치역(range)이 $Y$라면, 이를 전사 함수(onto)라고 부릅니다.
만약 함수 $\phi$가 one-to-one이면서 동시에 onto라면, 이를 일대일 대응(one-to-one correpondence)이라고 부릅니다.
만약 함수 $\phi$에 있는 모든 순서쌍 $(x, y)$를 $(y, x)$와 같이 앞 뒤를 바꿔도 함수의 정의에 부합한다면, 이 함수를 $\phi$의 역함수(inverse function)라고 하며, $\phi ^ {-1}$와 같이 표기합니다.
당연하게도, 역함수는 기존 함수가 일대일 대응일 때만 잘 정의가 됩니다. 왜냐하면, 모든 순서쌍들의 앞 뒤를 바꾼 집합이 함수의 정의에 부합하려면, 기존 순서쌍들이 모두 $x$하나에 $y$하나만 매칭되야 하기 때문입니다.
일대일 대응을 사용한다면, 위에서 언급한 집합의 크기(Cardinality)를 무한 집합으로도 확장시킬 수 있습니다.
위에서 정의한 바에 따르면, 집합의 Cardinality는 그 집합의 원소의 개수라고 했습니다.
하지만, 무한 집합은 그 원소의 개수가 무한합니다. 여기서는 정수 집합 $\mathbb {Z}$의 Cardinality를 $\aleph _0$라고 정의합니다.
그러면 다른 무한 집합의 Cardinality는 어떻게 정의할까요?
이는 Cardinality의 상등으로 정의할 수 있습니다.
- Cardinality의 상등
두 집합 $X$와 $Y$의 Cardinality가 서로 같다는 말은 두 집합 사이의 일대일 대응(one-to-one correspondence)이 존재함을 의미합니다.
유한 집합에서 두 집합의 크기가 같다를 논할 때, 두 집합의 원소 하나에 하나가 대응이 잘 됨을 생각해 본다면 Cardinality의 상등의 정의 또한 자연스러운 정의임을 알 수 있습니다.
예를 들어봅시다.
짝수 정수의 집합, 즉, $2\mathbb{Z} = \{ 2n \ | \ n \in \mathbb{Z} \}$는 어떤 Cardinality를 가질까요?
함수 $\phi$를 하나 생각해 봅시다. 이 함수는 $\mathbb{Z}$에서 $2\mathbb{Z}$로 대응되는 함수로, $\mathbb{Z}$의 원소 $n$을 $2n$로 보내는 함수입니다.
이 함수는 당연하게도 일대일 대응입니다.
따라서, 위의 Cardinality의 상등의 정의에 따라, $2\mathbb{Z}$의 Cardinality는 $\aleph _0$입니다.
또 다른 예시를 들어봅시다.
이번엔 양의 정수 집합 $\mathbb{Z} ^{+}$을 생각해 봅시다.
함수 $\phi : \mathbb{Z} \rightarrow \mathbb{Z} ^ {+}$를 생각해봅시다. 이 함수는 $\mathbb{Z}$의 원소 $n$이 $0$보다 크거나 같다면 $2n+1$로, $n$이 $0$보다 작다면 $-2n$으로 대응시키는 함수입니다.
이 함수는 아래 그림에서 볼 수 있듯, 일대일 대응입니다.

따라서, $| \mathbb{Z} ^{+} | = \aleph _0$입니다.
이번엔 유리수 집합 $\mathbb{Q}$를 생각해 봅시다.
만약 이 집합을 아래 그림과 같이 $\mathbb{Z} ^{+}$에 $\mathbb{Q}$로 대응을 시킨다면, 일대일 대응을 만들 수 있습니다.

따라서, $| \mathbb{Q} | = \aleph _0$입니다.
놀랍게도, 짝수 정수의 집합, 정수의 집합, 유리수 집합 모두 Cardinality가 같음을 알 수 있습니다.
이는 우리 직관에 상당히 반하는 일인데, 유리수 집합은 정수 집합을 포함하고 있고, 정수 집합은 짝수 정수의 집합을 포함하고 있기 때문입니다.
때문에 그 Cardinality가 서로 대소관계를 가질 것이라 생각하지만, 실제론 그렇지 않습니다.
이번엔 실수 집합 $\mathbb{R}$을 생각해 봅시다.
이 집합 또한 $\mathbb{Z} ^{+}$와 잘 대응시킨다면, $| \mathbb{R} | = \aleph _0$임을 보일 수 있을까요?
하지만, 이는 불가능합니다.
집합 $S = \{ x \in \mathbb{R} \ | \ 0 < x < 1 \}$가 Cardinality $\aleph _0$를 가지고 있다고 생각해 봅시다.
그러면, 우리는 위에서 했던 것처럼 $S$의 모든 원소들을 일렬로 "나열"할 수 있을 것입니다.

이 리스트에서 첫 번째 원소의 첫번째 자릿수와 다른 숫자를 취하고, 두번째 원소의 두번째 자리수와 다른 숫자를 취하고, 그런 식으로 $N$번째 원소의 $N$번째 자리수와 다른 숫자를 취해서 만든 수 $x$를 생각해 봅시다.
$x$는 이 리스트의 어떠한 수를 가지고 오든지 간에 그 수와 다른 자릿수가 존재합니다.
따라서, $x$는 이 리스트에 존재하지 않지만, $S$의 원소이므로, 이는 모순입니다.
따라서, $|S| \neq \aleph _0$입니다.
또한, 함수 $\phi : (0, 1) \rightarrow \mathbb{R}, \phi (x) = \mathrm{tan} \pi (x - \frac{1} {2})$을 생각해 봅시다.
이 함수는 일대일 대응이므로, $|S| = | \mathbb{R} |$임을 알 수 있습니다.
따라서, $| \mathbb{R} | \neq \aleph _0$입니다.
때문에 우리는 실수 집합 $\mathbb{R}$의 크기를 그냥 $| \mathbb{R} |$이라고 표기합니다.
부등호를 사용한다면, $\aleph _0 < | \mathbb{R} |$임을 알 수 있습니다.
다시 말해, 정수 집합의 크기보다 실수 집합의 크기(Cardinality)가 더 큼을 알 수 있습니다. 사실은, 실수 집합의 크기보다 더 큰 집합은 얼마든지 있으며, 그 집합보다 더 큰 집합이 "무한히" 존재함은 어떤 집합 $S$가 그 집합의 부분 집합들을 모두 모아놓은 집합, 즉, 멱집합 $2^{S}$과 항상 일대일 대응을 만들 수 없음을 보여줌으로써 증명할 수 있습니다.
이에 대한 증명은 독자 여러분에게 맡기겠습니다.
마지막으로, Relation으로 돌아와서, 이 단원에서 가장 중요한 동치 관계(Equvalence Relation)와 동치류(Equvalence class), 그리고 분할(Partition)에 대해 알아봅시다.
-분할(Partition)
집합 $S$의 분할(Partition)은 공집합이 아닌 $S$의 부분 집합들을 모아놓은 집합으로, $S$의 원소 $a$마다 정확히 하나의 Partition의 원소($S$의 부분 집합)에 속하는 집합입니다.
Partition의 원소는 cell이라고 말합니다.
또한, 어떤 원소 $x$를 포함하는 cell은 $\bar{x}$와 같이 표기합니다.
어렵게 쓰여 있지만, 사실 아래 그림과 같이, 어떤 집합 $S$가 있다면 이를 케이크 자르는 것 마냥 분할해 놓은 것을 의미합니다.
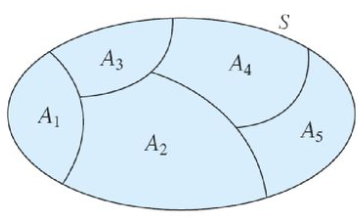
말 그대로 "분할"(Partition)인 것입니다.
예를 들어볼까요?
$\mathbb{Z} ^ {+}$을 짝수와 홀수로 분리한다면, 짝수 집합과 홀수 집합은 서로 Disjoint하고, 두 집합을 합치면 $\mathbb{Z} ^ {+}$를 이루므로, 이 집합들이 $\mathbb{Z} ^ {+}$에 대해서 Partition을 이루고 있다고 이야기할 수 있습니다.
이 개념을 확장시켜서, 만약 $3$으로 나눈 나머지가 $0, 1, 2$일 때로 분리한다면 어떻게 될까요?
$3$으로 나눈 나머지가 $0$인 집합, $1$인 집합, $2$인 집합은 모두 Disjoint 하며, 모든 집합을 합치면 $\mathbb{Z} ^ {+}$이 되므로, 이 또한 Partition을 이루고 있다고 할 수 있습니다.
일반화를 시키면, 우리는 $\mathbb{Z} ^{+}$를 $n$으로 나누었을 때의 나머지들$(0, 1, ... n-1)$로, 즉, $n$개의 cell들로 분할시킬 수 있습니다. 이를 $n$에 대한 잉여류(Residue Classes for modulo $n$)라고 부릅니다.
Partition을 곰곰이 생각해 보면, 같은 cell에 있는 원소들은 모두 다음과 같은 3가지 조건을 만족함을 알 수 있습니다.
1. $\bar{x}$에는 $x$가 있습니다.
2. 어떤 cell에 $x$가 있고, $y$가 있으면, 그 cell에는 $y$도 있고 $x$도 있습니다.
3. 어떤 cell에 $x$가 있고, $y$가 있으며, $y$가 있고 $z$가 있으면, 그 cell에는 $x$도 있고 $z$도 있습니다.
너무나도 당연한 이야기입니다.
예를 들어, $2$와 $4$가 짝수집합에 있고, $4$와 $6$이 짝수 집합에 있다면 $2$와 $6$은 모두 짝수 집합에 있을 것입니다.
이렇게 당연한 이야기를 Relation으로 확장을 시킨 것이 동치 관계(Equivalence Relation)입니다.
-동치 관계(Equivalence Relation)
집합 $S$에서 정의된 Relation $\mathscr{R}$이 모든 $x, y, z \in S$에 대해 다음 3가지 조건을 만족한다면 동치 관계(Equivalence Relation)라 부릅니다.
1. 반사 관계(Reflexive) $x \mathscr{R} x$
2. 대칭 관계(Symmetric) 만약 $x \mathscr{R} y$면, $y \mathscr{R} x$
3. 추이 관계(Transitive) 만약 $x \mathscr{R} y$이고, $y \mathscr{R} z$이면, $x \mathscr{R} z$이다.
이런 동치관계의 예시를 들어볼까요?
위에서 이야기했던 Equality Relation또한, 동치관계의 훌륭한 예시가 됩니다.
또한, 위에서 이야기 했던 Residue Classes modulo $n$에 의해 나뉜 Partition들에 대응이 되는 Equivalence Relation, 즉, $a$와 $b$의 나머지가 같을 때를 Relation으로 삼는다면, 이 또한 Equivalence Relation이 됩니다.
이 경우, 특별히 이 Relation을 "Congruence Modulo $n$", 즉, $n$에 대한 합동이라고 이야기합니다.
위의 두 가지 예시가 왜 동치관계를 만족시키는지에 대한 내용은 독자 여러분들에게 맡기겠습니다.
마지막으로, 이 단원의 핵심, Equivalence Relation과 Partition사이의 관계를 나타내는 증명을 보고 이 글을 마치고자 합니다.
- Equivalence Relation and Partitions
$S$가 공집합이 아닌 집합이라고 합시다. 그리고, $\sim$를 $S$위에서 정의된 Equivalence Relation이라고 합시다.
그러면, $\sim$은 $S$위에서 Partition을 형성합니다.
다시 말해, $\bar{a} = \{ x \in S \ | \ x \sim a \}$가 Partition의 cell이 됩니다.
또한, $S$위에서 Partition이 형성되어 있다면, $a$와 $b$가 같은 cell에 있을 때 $a \sim b$라고 Relation $\sim$을 정한다면, 이는 Equivalence Relation이 됩니다.
어렵게 쓰여 있지만, 곰곰이 생각해 보면 당연한 내용인 것처럼 보입니다.
쉽게 이야기하자면, 같은 cell에 있는 원소들끼리는 "같다"라고 간주하는 것입니다.
예를 들어, "$5$로 나눈 나머지"라는 관점에서 봤을 때에는 $6$이나 $1$이나 같은 것이죠.
이 정리에 대한 의미가 이렇다는 것이고 이 정리에 대한 증명은 Equivalence Relation과 Partition의 정의를 적극적으로 활용하여 증명합니다.
증명은 다음과 같습니다.
$( \Rightarrow )$ 먼저, $\bar{a} = \{ x \in S \ | \ x \sim a \}$들이 모두 $S$에 대해 Partition을 형성함을 보입시다.
그러려면, 다음과 같은 두 가지 사실을 보이면 됩니다.
1. 모든 $a \in S$에 대해 $a$가 들어있는 cell이 존재한다.
2. 한 원소는 서로 다른 cell에 동시에 속해있어서는 안 된다.
Proof of 1) $\sim$은 반사적(Reflexive) 관계이기 때문에, 어떠한 $a \in S$를 가져와도 $a \sim a$를 만족합니다. 따라서 $a$는 위의 $\bar{a}$정의에 의하여 $\bar{a}$에 속하게 됩니다.
Proof of 2) 만약 $a \in \bar{b}$라고 해봅시다. 우리가 보여주고 싶은 것은 $\bar{a} = \bar{b}$라는 사실입니다.
다시 말하자면, $a$라는 원소가 $\bar{b}$라는 cell에 있다면, 그 cell은 사실 $\bar{a}$과 같다는 말입니다.
먼저, $\bar{a} \subseteq \bar{b}$임을 보입시다. 다시 말해, 어떤 원소가 $\bar{a}$에 있다면, 그 원소가 $\bar{b}$에도 있음을 보이면 됩니다. 즉, $x \in \bar{a}$라면 $x \in \bar{b}$임을 보이면 됩니다.
$x \in \bar{a}$이므로, $x \sim a$입니다. 또한, 앞선 가정에 의해 $a \sim b$이고, 추이적(transitive) 관계에 의해 $x \sim b$입니다. 즉, $x \in \bar{b}$입니다.
두번째로, $\bar{b} \subseteq \bar{a}$임을 보입시다. $x \in \bar{b}$이면, $x \sim b$입니다. 또한, 앞선 가정에 의해 $a \sim b$이고, 대칭적(symmetric) 관계에 의해 $b \sim a$입니다. 따라서, 추이적(transitive) 관계에 의해 $x \sim a$입니다. 따라서, $x \in \bar{a}$입니다.
$( \Leftarrow )$ 이에 대한 증명은 위에서 이미 이야기가 된 내용입니다.
따라서, 어떤 동치 관계가 정의가 되어있다면, 그로부터 "같은 부류"들끼리 묶을 수 있으며, 이러한 묶음들은 집합을 "분할"함을 수학적으로 증명하였습니다.
우리는 한 동치 관계로부터 나온 cell들을 "동치류(Equvalence Class)"라고 부를 것입니다.
대표적으로, 위에서 이야기 한 $\mathbb{Z} ^{+}$에 대한 Residue classes modulo $n$ 는 동치류입니다.
다음 섹션에서는 대수적 구조가 무엇인지에 대해 간단한 소개를 하고, 다양한 예시들, 그중에서 복소수의 곱셈을 중점으로 알아보겠습니다.
'공부 기록 > 대수학' 카테고리의 다른 글
| [대수학] 2. Binary Operations (0) | 2023.07.22 |
|---|---|
| [대수학] 1. Introduction and Examples (0) | 2023.06.30 |

