https://www.acmicpc.net/problem/16958
16958번: 텔레포트
2차원 평면 위에 N개의 도시가 있다. 일부 도시는 특별한 도시이다. (r1, c1)에 있는 도시에서 (r2, c2)에 있는 도시로 가는 이동 시간은 |r1 - r2| + |c1 - c2|와 같다. 만약, 두 도시가 특별한 도시라면, 텔
www.acmicpc.net
22/10/27
다양한 풀이가 존재하는 문제로, 파이썬으로 풀기 위해서는 별의별 최적화를 다 해야 되는 문제이다.
나이브한 플로이드-워셜 알고리즘으로 접근한다면 파이썬에서는 TLE를 받을 수밖에 없기 때문에 무조건적인 최적화가 필요하다.
이 글에서는 2가지 풀이 방법을 소개할 것이다.
첫 번째 문제 접근 방식:
이 문제를 먼저 접했을 때, 도시의 수의 최대 개수가 1000개이기 때문에 플로이드-워셜을 돌리면 1000*1000*1000으로 아슬아슬하게 통과할 것이라고 생각하고, 그리고 코드를 짰다.
코드의 흐름은 대충 다음과 같다.
텔포 가능한 여부까지 노드를 저장하는 곳에 저장한 후, graph[i][j]를 i노드에서 j노드로 가는 택시 거리로 초기화시켜주었다.
이후 플로이드-워셜을 돌리는데, 만약 시작 노드와 도착 노드가 모두 텔레포트가 가능한 노드라면, 텔레포트를 하는데에 드는 시간(T)까지 고려하여 min함수를 사용하여 graph[i][j]를 갱신한다.
만약 그게 아니라면, 그냥 중간 노드를 거쳐가는 것으로 갱신한다.
결과는 당연히 TLE.
플로이드-워셜로 접근하기 위해서는 최적화된 코드가 필요했다.
먼저 첫 번째로, 플로이드-워셜을 돌릴 때, 항상 if문을 사용했다.
이전에는 min함수를 사용하여 최솟값을 갱신해주었다.
이는 1000*1000*1000번의 횟수로 함수를 불러오는 것인데, 이렇게나 많이 함수를 반복해서 호출하는 것은 시간을 많이 잡아먹는다.
때문에 min함수를 호출하는 대신, if문으로 대소 비교를 하여 갱신하도록 해주었다.
두 번째로, 이전에 graph를 선언할 때에 INF = 1e10로 초기화하여 선언을 했는데, INF값을 10000(적당히 큰 값)으로 바꿔주었다.
너무나 큰 값으로 초기화를 하는 것은 시간이 더 걸린다고 생각했기 때문이다.(자세한 이유는 나도 모르나, 왠지 그럴 것 같아서 바꿔주었다.)
세 번째로, 그래프에 간선의 값들을 넣을 때(초기화 작업을 할 때), 둘 다 텔레포트가 가능한 곳이고, 텔레포트로 가는 게 더 이득이라면, 그냥 초기화 작업할 때 텔레포트로 가는 시간을 넣어두었다.
이전에는 플로이드-워셜 작업을 할 때, 텔레포트가 가능한지 여부를 판별했었다.
그러면 그 여부를 판별하는 작업을 총 1000*1000*1000번이나 하게 되는 셈인데, 굳이 그럴 필요가 없다고 생각했기 때문이다.
때문에 초기화 작업을 할 때, 둘 다 텔레포트가 가능한 곳이고 텔레포트하는 게 더 이득이면 그걸로 초기화를 시켜주었다.
초기화 작업은 대략 1000*1000번을 하기 때문에 시간적으로 더 줄일 수 있다.
마지막으로, 초기화 작업을 할 때, 이중 for문 대신에 itertools의 combinations를 사용하여 더 줄였다.
어차피 양방향 간선이라는 사실을 우리는 알고, 그 간선의 가중치 또한 같다는 사실을 알고 있기 때문에, 같은 값을 가지는 간선이 2개라는 사실을 알고 있다.
다시 말해, i에서 j로 가는 간선의 가중치나 j에서 i로 가는 간선의 가중치는 같다.
이를 이용하여, 중복되는 애들을 제거하는 combinations를 사용하면 시간을 조금 더 줄일 수 있으리라 생각했다.
이런 4가지의 최적화 작업을 거치고 난 후에서야 pypy3에서 간신히 AC를 받을 수 있었다.
아래는 내가 위의 접근 방식과 같이 작성한 파이썬 코드이다. 더보기를 누르면 확인할 수 있다.
# 16958번 텔레포트
# 그래프 이론, 그래프 탐색, 플로이드-워셜
import sys
input = sys.stdin.readline
from itertools import *
INF = 10000
N, T = map(int, input().rstrip().split())
nodes = []
for _ in range(N):
s, x, y = map(int, input().rstrip().split())
nodes.append([s, x, y])
graph = [[INF for _ in range(N)] for _ in range(N)]
for i, j in combinations(range(N), 2):
manhattan_distance = abs(nodes[i][1]-nodes[j][1]) + abs(nodes[i][2]-nodes[j][2])
graph[i][j] = manhattan_distance
graph[j][i] = manhattan_distance
if nodes[i][0] and nodes[j][0] and T < manhattan_distance:
graph[i][j] = T
graph[j][i] = T
for k in range(N):
for i in range(N):
for j in range(N):
if graph[i][k] + graph[k][j] < graph[i][j]:
graph[i][j] = graph[i][k] + graph[k][j]
M = int(input())
for _ in range(M):
start, end = map(int, input().rstrip().split())
print(graph[start-1][end-1])
두 번째 문제 접근 방식:
두 번째 문제 접근 방식은 거리 함수의 성질을 이용한 풀이이다.
그전에 먼저, 거리 함수에 대해서 알아야 한다.
거리 함수란 무엇인가?라고 한다면 다음과 같은 3가지 조건을 만족시키는 함수를 거리 함수라고 한다.
1. 어떤 점에서 다른 점으로부터 잰 거리가 0이라는 말은 두 점이 서로 같은 점이라는 말과 같다.
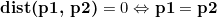
2. 어떤 점 p1에서 다른 점 p2로부터 잰 거리는 p2에서 p1으로부터 잰 거리와 같다.

3. 중간 점 p3를 거쳐서 잰 거리는 p1과 p2를 바로 잰 거리보다 같거나 크다. (삼각 부등식)

대표적인 거리 함수로 우리가 자주 쓰는 유클리드 거리(Euclidean distance)가 있다.
모두가 잘 알고 있듯, 평면 위에서의 유클리드 거리는 다음과 같다.

그리고, 이 식은 거리 함수의 정의를 모두 만족시킨다.

어렵게 생각할 필요가 없다.
삼각 부등식이라는 것도, 결국 위의 그림처럼 중간에 한 점을 거치면 더 오래 걸린다는 것이 아닌가?
그리고 "거리" 함수라는 말에서 보았듯, 자기 자신과 잰 거리는 0이고, 점에서 점으로부터 잰 거리는 a에서 b로 재나, b에서 a로 재나, 항상 같을 것이다.
이러한 당연한 거리의 성질을 정의로써 규격화시킨 것이 "거리 함수"라고 보면 될 것이다.
이 문제에서는, 한 도시에서 다른 도시로 가는 데에 드는 시간은 곧 한 점에서 다른 한 점으로 가는 택시 거리와 같다는 사실을 잘 알 수 있다.
택시 거리(또는 맨하탄 거리) 또한, 위의 3가지 거리 함수의 정의를 모두 만족시키는 "거리 함수"이다.
택시 거리는 다음과 같이 정의가 된다.

택시 거리가 거리 함수의 첫 번째와 두 번째 조건을 만족한다는 사실은 자명하다.
택시 거리가 거리 함수의 세 번째 조건을 만족한다는 사실을 증명해보자.



때문에 택시 거리는 거리 함수의 모든 조건을 만족시킨다.
문제의 내용을 다시 상기시켜보자.
어떤 한 점에서 다른 한 점으로 가는 데에 걸리는 시간은 곧 어떤 한 점에서 다른 한 점으로부터의 택시 거리와 같고, 따라서 삼각 부등식을 만족시킨다.
이 말은 곧, 어떤 한 점으로부터 다른 한 점까지 가는 데의 최소 거리는 중간 점을 거치지 않고 그냥 가는 것과 같다.
근데, 플로이드-워셜의 원리를 생각해보자.
플로이드-워셜의 원리는 시작점과 도착점이 있으면, 그 둘을 제외한 모든 중간점들을 고려하여 (시작점과 중간점 사이의 가중치 + 중간점과 도착점 사이의 가중치)와 (시작점과 도착점 사이의 가중치) 중 최소 값으로 갱신하는 원리이다.
근데, 만약 시작점도 그렇고, 도착점도 그렇고 둘 다 텔레포트가 불가능하다면, (첫 번째 풀이에 따르자면) 시작점과 도착점 사이의 가중치는 그냥 시작점과 도착점 사이의 거리로 초기화가 될 것이다.
근데, 앞서 언급했듯, 그러면 중간점을 거치는 게 항상 손해이다!
그러면, 플로이드-워셜을 굳이 안 돌려도 되는데, 돌려서 시간 낭비가 되는 것이다.
이게 기본적인 아이디어이다.
만약, 이 문제에서 텔레포트가 없었더라면 플로이드-워셜을 돌릴 이유도 없다. 항상 중간점을 거치는 게 손해이기 때문에 그냥 시작점에서 도착점으로 가는 거리를 출력해주면, 그것이 곧 시작점에서 도착점으로 가는 최단 시간이 된다.
하지만, 텔레포트의 유무로 인해 경우의 수가 총 4가지로 나뉘게 된다.
이는 다음과 같다.
1. 시작 노드, 도착 노드 모두 텔레포트 불가능한 경우
2. 시작 노드는 텔레포트가 가능하고, 도착 노드는 텔레포트가 불가능한 경우
3. 시작 노드는 텔레포트가 불가능하고 도착 노드는 텔레포트가 가능한 경우
4. 시작 노드와 도착 노드 모두 텔레포트 가능한 경우
첫 번째 경우를 그림으로 살펴보자.

이 그림에서 검은 점은 텔레포트가 불가능한 점이고, 빨간 점은 텔레포트가 가능한 점이다.
시작점에서 도착점으로 가는데, 두 점이 모두 불가능하면 최소거리는 그냥 두 점 사이의 거리와 같다.
다시 말해 중간 노드를 거치지 않아도 된다.
따라서 최소 거리는 그냥 dist(S, E)가 된다.
두 번째 경우를 살펴보자.

그림에서 볼 수 있듯, 검은 점들을 거쳐서 가는 것은 손해다. 따라서 빨간 점들만 고려하면 된다.


만약 텔레포트를 사용한다면, 최대한 도착지점과 가까운 곳까지 텔레포트를 하고, 그 이후에 걸어가는 것이 이득이라는 사실을 알고 있다.
따라서, 텔레포트가 가능한 곳들 중 도착 지점과 가장 가까운 지점을 M이라고 하면, dist(M, E) + T와 dist(S, E)중 최솟값을 취하면 그것이 곧 최소 시간이 된다.
비슷한 논리로, 만약 도착 노드만 텔레포트 가능한 경우라면, 아래 그림과 같다.

만약 둘 다 텔레포트가 가능한 경우라면, 중간 노드를 고려할 필요도 없다.
왜냐하면 중간 노드가 텔레포트가 가능하지 않은 경우라면 더더욱 고려도 할 필요가 없고, 텔레포트가 가능한 경우라고 할지라도, 텔레포트를 2번 하는 것보다는 그냥 시작 노드에서 도착 노드로 텔레포트 한 번 하는 게 더 낫기 때문이다.
따라서 이때의 최소 시간은 min(dist(S, E), T)가 된다.
정리를 하자면 다음과 같다.
1. 시작 노드와 도착 노드 모두 텔레포트 가능한 경우
min(dist(start, end), T)
2. 시작 노드만 텔레포트가 가능한 경우
텔레포트 가능한 곳 중 도착 노드랑 가장 가까운 곳을 mid라고 할 때,
min(dist(start, end), dist(mid, end) + T)
3. 도착 노드만 텔레포트가 가능한 경우
텔레포트 가능한 곳 중 시작 노드랑 가장 가까운 곳을 mid라고 할 때,
min(dist(start, end), dist(start, mid) + T)
4. 둘 다 텔레포트 불가능할 때
dist(start, end)
자, 이제 풀이의 거의 마지막까지 왔다.
앞서 풀이를 봤듯, 최단 시간을 구할 때에는 텔레포트가 가능한 점들만 고려를 했었다.
이를 응용하여, 이제 우리는 node_value라는 리스트를 하나 정의를 할 것이다.
이 리스트의 인덱스는 노드 번호를 의미하고, 그 인덱스에 해당하는 값은 그 노드에서 제일 가까운 "텔레포트 가능한 노드"와의 거리를 담을 것이다.
만약 노드가 텔레포트 가능한 노드라면, 그 노드에서 제일 가까운 "텔레포트 가능한 노드"는 자기 자신이므로 0이 나올 것이다.
만약 노드가 텔레포트 가능하지 않은 노드라면, 그 노드에서 제일 가까운 "텔레포트 가능한 노드"와 그 노드 사이의 거리가 node_value 리스트에 담길 것이다.
따라서 node_value리스트를 구성하는 전처리 작업을 거쳐주기만 하면, 위의 네 가지 경우를 모두 포함하는 식이 다음과 같이 나오게 된다.
min(dist(start, end), node_values[start] + T + node_values[end])
이를 이용하여 문제를 해결하면 된다.
아래는 내가 위의 접근 방식과 같이 작성한 파이썬 코드이다. 더보기를 누르면 확인할 수 있다.
# 16958번 텔레포트
# 그래프 이론, 그래프 탐색, 플로이드-워셜
'''
개선된 풀이: (cinador님의 풀이 참고)
거리함수의 성질을 이용함.
거리 함수는 항상 삼각 부등식이 성립함.
dist(a, b) + dist(b, c) >= dist(a, c)
이 부등식에 따르자면,
중간 노드가 텔레포트를 못하는 노드인 경우면,
중간에 노드 거치는게 무조건 손해다.
시작 노드, 도착 노드, 중간 노드 모두 텔레포트가 되는 경우면,
텔레포트를 두 번 하는건 손해이다.
그래서 플로이드-워셜을 쓰는게 손해일 때가 많다.
그렇다면, 플로이드 워셜을 아주 살짝만 변형시켜보자.
어떤 노드에서 다른 노드로 가는 최소 거리는 다음과 같다.
1. 시작 노드와 도착 노드 모두 텔포 가능한 경우
min(dist(start, end), T)
2. 시작 노드만 텔포가 가능한 경우
텔포 가능한 곳 중 도착 노드랑 가장 가까운 곳을 mid라고 할 때,
min(dist(start, end), dist(mid, end) + T)
3. 도착 노드만 텔포가 가능한 경우
텔포 가능한 곳 중 시작 노드랑 가장 가까운 곳을 mid라고 할 때,
min(dist(start, end), dist(start, mid) + T)
4. 둘다 텔포 불가능 할때
dist(start, end)
'''
import sys
input = sys.stdin.readline
from itertools import combinations
def dist(x1, y1, x2, y2):
return abs(x1-x2) + abs(y1-y2)
INF = 10000
N, T = map(int, input().rstrip().split())
total_nodes = []
teleport_nodes = []
node_values = []
for i in range(N):
s, x, y = map(int, input().rstrip().split())
total_nodes.append([x, y])
if s:
teleport_nodes.append([x, y])
# 아래 과정을 통해 각 노드별 value를 저장함
# 만약 teleport가 가능한 노드라면, node_value가 0이 나올 것임
# 만약 teleport가 가능하지 않은 노드라면, 제일 가까운 텔레포트 가능한 노드 사이의 거리가 node_value가 됨.
for point in total_nodes:
x1, y1 = point
node_value = INF
for teleportable_point in teleport_nodes:
x2, y2 = teleportable_point
distance = dist(x1, y1, x2, y2)
if distance < node_value :
node_value = distance
node_values.append(node_value)
M = int(input())
for _ in range(M):
start, end = map(int, input().rstrip().split())
x1, y1 = total_nodes[start-1]
x2, y2 = total_nodes[end-1]
print(min(dist(x1, y1, x2, y2), node_values[start-1] + T + node_values[end-1]))'알고리즘 > 백준 문제 풀이' 카테고리의 다른 글
| [Python] 25793번 초콜릿 피라미드 (0) | 2022.11.06 |
|---|---|
| [Python] 5011번 Robots on a grid (0) | 2022.11.05 |
| [Python] 11869번 님블 (0) | 2022.11.02 |
| [Python] 16899번 채석장 게임 (0) | 2022.11.02 |
| [Python] 25591번 푸앙이와 종윤이 (0) | 2022.11.01 |
