https://www.acmicpc.net/problem/25793
25793번: 초콜릿 피라미드
코코는 특이하게 생긴 화이트 초콜릿과 다크 초콜릿을 무한히 많이 갖고 있다. 화이트 초콜릿은 각 모서리의 길이가 1인 사각 피라미드이고, 다크 초콜릿은 각 모서리의 길이가 1인 정사면체 모
www.acmicpc.net
22/10/15
전형적인 수학 문제로, $O(1)$의 시간 복잡도로 문제를 해결해야 풀 수 있다.
문제 접근 방식:
아래 그림을 보자. 아래 그림은, $2*3$ 피라미드의 한 층을 채우는 과정을 도식화한 것이다.
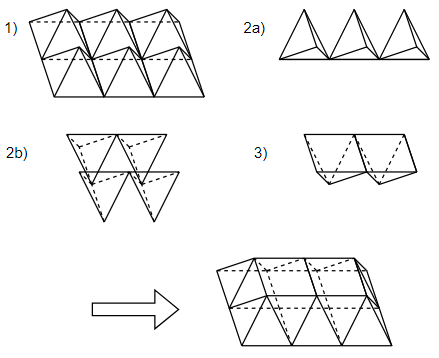
이 그림을 이용해, 예시를 하나 들어보겠다.
만약 $R = 3$, $C = 4$라면, 다음 그림과 같은 모습을 띄게 될 것이다.
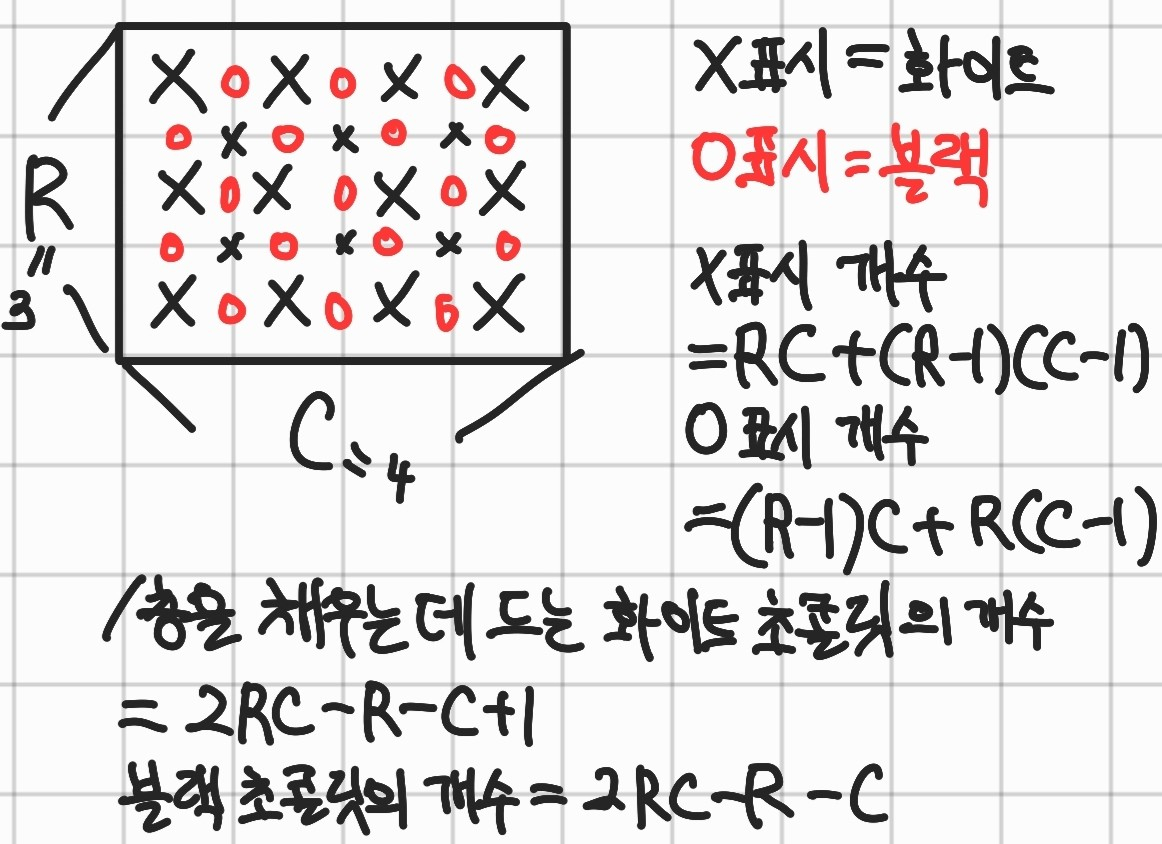
이 그림은 $3*4$ 피라미드의 한 층을 채우는 데에 놓는 화이트 초콜릿의 위치를 검은색 X 표시로, 다크 초콜릿의 위치를 빨간색 O표시로 나타낸 것이다.
검은색 X표시는 $3*4 + 2*3$개이므로, 이를 일반화한다면, $RC + (R-1)(C-1)$개라고 생각할 수 있다.
빨간색 O표시는 $2*4 + 3*3$개이므로, 이를 일반화 한다면, $(R-1)C + R(C-1)$개라고 생각할 수 있다.
우리는 한 층을 채우면, 이후 층의 가로는 $C-1$로 줄어들고, 세로는 $R-1$로 줄어듦을 알 수 있다.
예를 들어, 맨 위 그림의 $2*3$피라미드의 경우, 한 층을 채우고 난 후의 윗 면의 상황은 $1*2$로 바뀌게 된다.
때문에, 층을 채우는 작업을 우리는 총 $min(R, C)$번 하게 된다.
따라서, 피라미드를 모두 채우는데 드는 화이트 초콜릿 개수를 공식화시키면 다음과 같다.
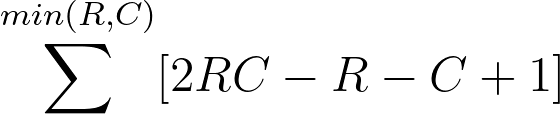
그러면, $min(R, C) = p$, $max(R, C) - min(R, C) = q$라고 하자.
우리는 그러면 $p$와 $p+q$로 $R$과 $C$를 나타낼 수 있다.
때문에, 다음과 같이 나타낼 수 있다.

이 공식을 정리하자면 다음과 같이 표현할 수 있다.

합 공식을 이용하여 이 식을 전개하면 다음과 같다.

이것이 화이트 초콜릿의 총 개수가 된다.
다크 초콜릿의 총 개수는 저 식에서 맨 뒤의 $p$만 빼면 된다.
이를 이용하여 총 개수를 구할 수 있다.
아래는 내가 위의 접근 방식과 같이 작성한 파이썬 코드이다. 더보기를 누르면 확인할 수 있다.
# 초콜릿 피라미드
'''
접근 방법:
R값과 C값이 주어져 있을 때,
한 층을 채우는 화이트 초콜릿의 개수는 2*R*C - R - C + 1개
다크 초콜릿의 개수는 2*R*C - R - C개
'''
import sys
input = sys.stdin.readline
for _ in range(int(input())):
R, C = map(int, input().rstrip().split())
m, n = max(R, C), min(R, C)
k = m - n
white = n*(n+1)*(2*n+1)//3 - n*(n+1) + n*(n+1)*k - n*k + n
black = n*(n+1)*(2*n+1)//3 - n*(n+1) + n*(n+1)*k - n*k
print(white, black)'알고리즘 > 백준 문제 풀이' 카테고리의 다른 글
| [Python] 25918번 북극곰은 괄호를 찢어 (0) | 2022.11.09 |
|---|---|
| [Python] 1737번 Pibonacci (0) | 2022.11.09 |
| [Python] 5011번 Robots on a grid (0) | 2022.11.05 |
| [Python] 16958번 텔레포트 (2) | 2022.11.04 |
| [Python] 11869번 님블 (0) | 2022.11.02 |

