728x90
https://www.acmicpc.net/problem/6786
25/12/14
최대 유량 기초 문제이다. 모델링을 잘 하는 것이 관건이다.
문제 접근 방식:
문제를 정리하면 다음과 같다.
1. 모든 RH- "피"는 RH+, RH- "사람" 상관 없이 줄 수 있음.
2. O형 "피"는 A, B, AB, O "사람" 상관 없이 줄 수 있음.
3. A형 "피"는 A, AB "사람" 상관 없이 줄 수 있음.
4. B형 "피"는 B, AB "사람" 상관 없이 줄 수 있음.
5. AB형 "피"는 AB형 "사람"에게 줄 수 있음.
따라서, 일종의 이분 그래프처럼 "피"에서 "사람"으로 향하는 그래프를 모델링 할 수 있다.
그림으로 그리면 다음과 같다.
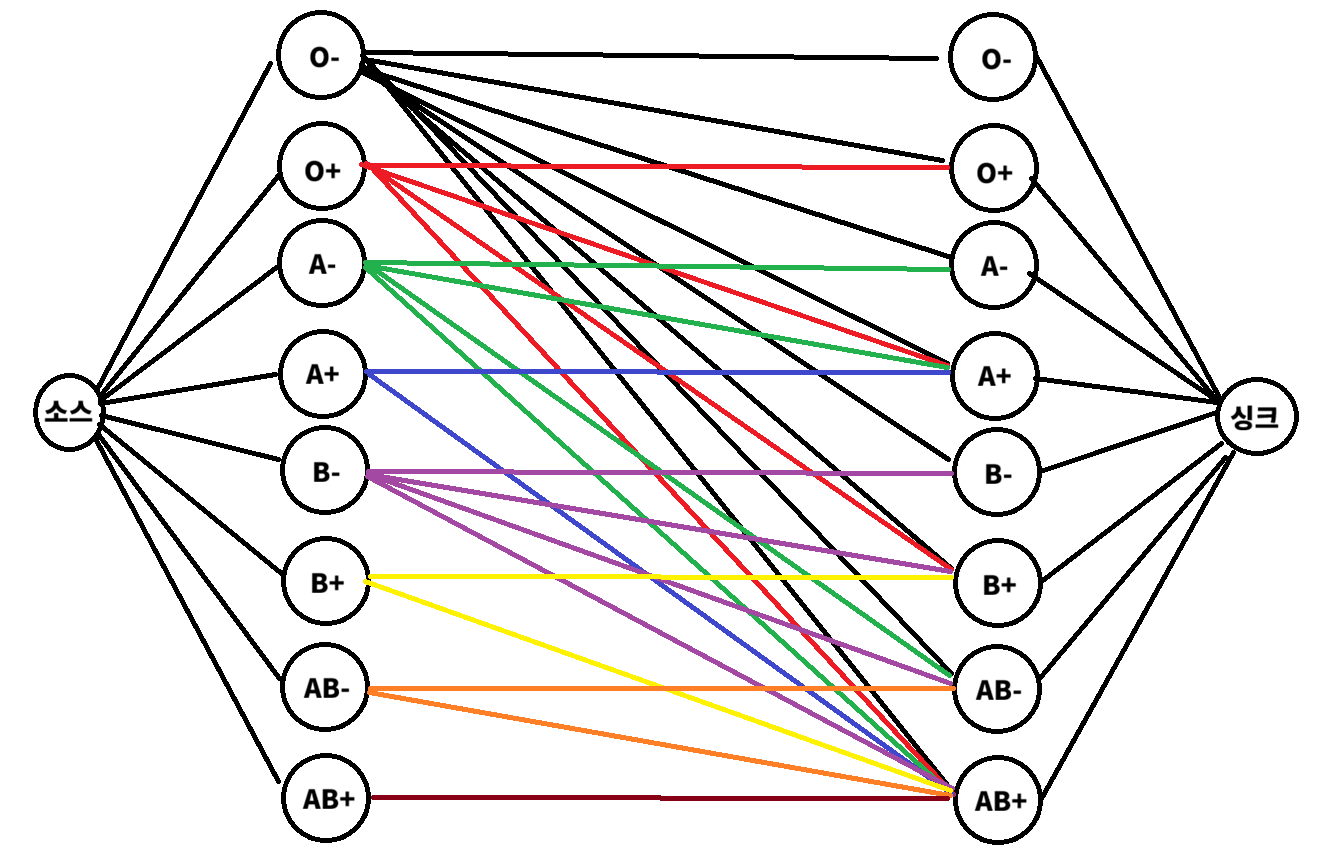
이때 간선의 용량을 정해야 한다.
소스에서 각 피로 향하는 간선의 용량은 문제에서 주어지는 피의 개수만큼 정해주고, 각 사람에서 싱크로 향하는 간선의 용량은 사람의 명수만큼 정해주면 된다.
그리고 그 외의 간선들의 용량은 INF로 처리하자.
아래는 내가 위의 접근 방식과 같이 작성한 C++ 코드이다. 더보기를 누르면 확인할 수 있다.
더보기
// 6786번 Blood Distribution
// 최대 유량 알고리즘 - 에드몬드 카프
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
#define INF 2'147'483'647
#define fastio ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
#define endl '\n'
struct Edge{
int target, capacity, flow; // 타겟, 용량, 유량
Edge* reverse; // 역방향 간선 참조하는 포인터
int residualCapacity() const { // 잔여 유량 계산
return capacity - flow;
}
void push(int amount){ // 유량 흘리기(갱신)
flow += amount;
reverse->flow -= amount;
}
};
void addEdge(int u, int v, int capacity, vector<vector<Edge*>>& graph){
Edge* uv = new Edge(); // u에서 v로 가는 간선 포인터
Edge* vu = new Edge(); // v에서 u로 가는 역방향 간선 포인터
// 정방향 간선 uv 초기화
uv->target = v;
uv->capacity = capacity;
uv->flow = 0;
uv->reverse = vu;
// 역방향 간선 vu 초기화
vu->target = u;
vu->capacity = 0;
vu->flow = 0;
vu->reverse = uv;
// 정방향과 역방향 둘다 넣어준다.
graph[u].push_back(uv);
graph[v].push_back(vu);
}
int BFS(int source, int sink, vector<Edge*>& reversedPath, vector<vector<Edge*>>& graph){
int N = graph.size();
vector<int> visited(N, 0);
vector<Edge*> parent(N); // 경로 역추적하기 위한 parent배열 선언.
queue<int> Q;
visited[source] = 1;
Q.push(source);
bool foundAugmentingPath = false;
while (!Q.empty() && !foundAugmentingPath){
int now = Q.front(); Q.pop();
for (Edge* edge: graph[now]){
int next = edge->target;
if (!visited[next] && edge->residualCapacity() > 0){ // 방문하지 않았고, 잔여 용량이 남아있다면
visited[next] = 1;
parent[next] = edge;
Q.push(next);
if (next == sink){ // sink로 도달가능하다면
foundAugmentingPath = true;
break;
}
}
}
}
if (!foundAugmentingPath){
return 0; // 더 이상 흘릴 유량이 없다.
}
reversedPath.clear();
int Flow = INF;
// 역방향 간선타고 가면서 흘릴 Flow 갱신
for (Edge* edge = parent[sink]; edge != nullptr; edge = parent[edge->reverse->target]){
Flow = min(Flow, edge->residualCapacity());
reversedPath.push_back(edge);
}
return Flow;
}
int EdmondKarp(int source, int sink, vector<vector<Edge*>>& graph){
int totalFlow = 0;
vector<Edge*> reversedPath;
while (int flow = BFS(source, sink, reversedPath, graph)){
for (Edge* edge : reversedPath){
edge->push(flow);
}
totalFlow += flow;
}
return totalFlow;
}
int main(void){
fastio
vector<vector<Edge*>> G(18);
vector<int> blood(8);
for (int i = 0; i < 8; ++i) cin >> blood[i];
vector<int> patient(8);
for (int i = 0; i < 8; ++i) cin >> patient[i];
for (int i = 0; i < 8; ++i){
addEdge(0, i+1, blood[i], G);
}
for (int i = 0; i < 8; ++i){
addEdge(9+i, 17, patient[i], G);
}
vector<pair<int, int>> edges = {{1, 9}, {1, 10}, {1, 11}, {1, 12}, {1, 13}, {1, 14}, {1, 15}, {1, 16},
{2, 10}, {2, 12}, {2, 14}, {2, 16},
{3, 11}, {3, 12}, {3, 15}, {3, 16},
{4, 12}, {4, 16},
{5, 13}, {5, 14}, {5, 15}, {5, 16},
{6, 14}, {6, 16},
{7, 15}, {7, 16}, {8, 16}};
for (auto p : edges){
addEdge(p.first, p.second, INF, G);
}
cout << EdmondKarp(0, 17, G);
return 0;
}728x90
'알고리즘 > 백준 문제 풀이' 카테고리의 다른 글
| [C++] 14398번 피타고라스 수 (0) | 2025.12.26 |
|---|---|
| [C++] 16590번 KMP (0) | 2025.12.24 |
| [C++] 22695번 Spirograph (0) | 2025.11.08 |
| [C++] 24558번 Downsizing (0) | 2025.10.21 |
| [C++] 34041번 회전체와 쿼리 (0) | 2025.10.20 |