https://www.acmicpc.net/problem/17597
25/01/12
간단한 기하학 문제다. 케이스를 나눠서 접근하면 쉽게 해결할 수 있다.
문제 접근 방식:
먼저 두 기둥을 잇는 케이블의 가장 짧은 길이는 두 기둥의 끝을 서로 이은 선분의 길이라는 사실은 쉽게 확인할 수 있다.
이제 케이블의 길이를 점점 늘린다고 해보자.
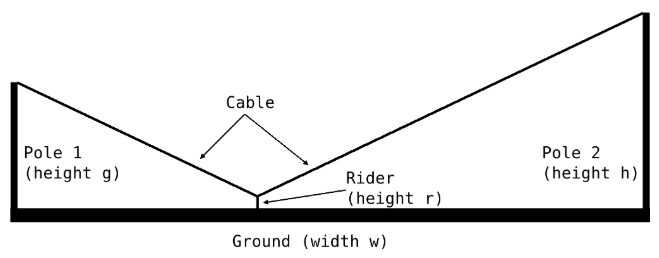
문제에서 주어지는 그림이 케이블을 점점 늘린 상황이라고 가정해보자.
우리는 이 때의 경우에도 케이블 카가 지면으로부터 $r$만큼 위에 있어야 한다는 사실을 알고 있다.
근데 문제는 최저점을 찍었을 때의 상황이 언제인지를 모른다. 케이블 카가 $x$만큼 오른쪽으로 간 상황이라고 해보자. 그러면 케이블의 길이가 다음과 같다.
$$l = \sqrt{(g-r)^2 + x^2} + \sqrt{(h-r)^2 + (w-x)^2}$$
케이블 카는 $0$부터 $w$지점까지 움직일 수 있다. 즉, $x$의 범위는 $0 \leq x \leq w$이다.
케이블이 길면 길수록 케이블 카는 지면으로부터 $r$만큼 위에 있지 못한다. 따라서, 조건을 만족하려면 케이블의 길이 $l$의 최솟값을 구해야 한다.
이는 이분 탐색 혹은 삼분 탐색으로 구할 수 있다.
따라서 문제에서 요구하는 케이블 길이의 최솟값은 $\sqrt{(h-g)^2 + w^2}$, 최댓값은 $\min(l)$이 된다.
C++에서는 iomanip헤더에서 fixed << setprecision()을 통해 뒤의 소숫점 자리수를 늘려서 출력할 수 있다.
아래는 내가 위의 접근 방식과 같이 작성한 C++ 코드이다. 더보기를 누르면 확인할 수 있다.
// 17597번 Zipline
// 기하학, 피타고라스 정리, 삼분 탐색
#include <iostream>
#include <cmath>
#include <iomanip>
using namespace std;
#define fastio ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
#define endl '\n'
typedef long long ll;
double f(ll w, ll g, ll h, ll r, double x){
return sqrt((double)(g-r)*(g-r) + x*x) + sqrt((double)(h-r)*(h-r) + (w-x)*(w-x));
}
void solve(int test_case_num){
ll w, g, h, r;
cin >> w >> g >> h >> r;
double a = sqrt((double)(max(g,h)-min(g,h))*(max(g,h)-min(g,h)) + (double)w*w);
double s = 0, e = w, m1, m2;
int loop = 1000;
while (loop){
m1 = (2*s + e)/3, m2 = (s + 2*e)/3;
if (f(w,g,h,r,m1) < f(w,g,h,r,m2)) e = m2;
else s = m1;
loop--;
}
cout << fixed << setprecision(8);
cout << a << ' ' << f(w,g,h,r,m1) << endl;
return;
}
int main(void){
int T; cin >> T;
for (int i = 1; i <= T; i++){
solve(i);
}
return 0;
}'알고리즘 > 백준 문제 풀이' 카테고리의 다른 글
| [Python] 2533번 사회망 서비스(SNS) (0) | 2025.02.27 |
|---|---|
| [C++] 7118번 Ones (0) | 2025.02.27 |
| [C++] 2143번 두 배열의 합 (0) | 2025.01.13 |
| [C++] 32999번 Ribbon on the Christmas Present (0) | 2025.01.12 |
| [C++] 33118번 ICPC Provincial (0) | 2025.01.11 |