https://www.acmicpc.net/problem/32871
24/12/03
좋은 아이디어를 가진 게임 이론 문제다.
문제 접근 방식:
문제 접근 방식의 핵심은, 행과 열의 쪼개진 부분을 붙여서 새로운 블록으로 생각해도 상관 없다는 것이다.
예를 들어, 다음과 같다.

$3 \times 4$크기의 판에서 $2$번 열을 선택해서 없앴다면,
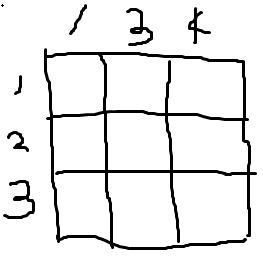
이렇게 그냥 새로운 $3 \times 3$짜리 크기의 판으로 생각해도 된다는 점이다.
편의 성을 위해, $N < M$이라고 가정하자.
그러면, 일단 $N = 1$인 경우 선공이 항상 이김은 당연하다.
$N = 2$이고 $M = 2$라면, 선공은 무슨 짓을 해도 $N = 1$인 경우로 되돌아가므로 선공이 진다.
$N = 2$이고 $M = 3$이라면, 선공은 $N=2, M=2$인 상태를 상대방에게 떠넘길 수 있으므로 선공이 이긴다.
$N = 2$이고 $M = 4$이라면, 선공은 $N=1$인 상태나 $N=2, M=3$인 상태를 상대방에게 넘겨야 되는데, 둘 다 이기는 포지션이라 선공이 진다.
$N=2$일 때 나머지의 경우는 충분히 유추가 가능할 것이다.
$N=3$이고 $M = 3$이라면, 선공은 무슨 짓을 해도 $N=2, M=3$인 상태를 상대방에게 넘겨야한다. 즉, 선공이 지게 된다.
$N=3$이고 $M = 4$이라면, 선공은 $N=3, M=3$인 상태를 상대방에게 떠넘길 수 있으므로 선공이 이긴다.
$N=3$이고 $M = 5$이라면, 선공은 $N=2, M=5$이거나 $N=3, M=4$인 상태를 상대방에게 넘겨야 되는데, 둘 다 이기는 포지션이라 선공이 진다.
$N=3$일 때 나머지의 경우도 충분히 유추할 수 있을 것이다.
이를 토대로 규칙을 보면, $N = 1$일때 선공이 무조건 이기며, $M-N$이 짝수인 경우 선공이 지고, 홀수라면 선공이 이긴다는 사실을 확인할 수 있다.
아래는 내가 위의 접근 방식과 같이 작성한 파이썬 코드이다. 더보기를 누르면 확인할 수 있다.
# 32871번 돌 게임 nm
# 게임 이론
import sys
input = sys.stdin.readline
ans = []
T = int(input())
for _ in range(T):
N, M = map(int, input().split())
if N > M: N, M = M, N
if N == 1: ans.append('YES')
elif (M-N) % 2 == 0: ans.append('NO')
else: ans.append('YES')
print(*ans, sep='\n')'알고리즘 > 백준 문제 풀이' 카테고리의 다른 글
| [C++] 26648번 물정수열 (0) | 2025.01.04 |
|---|---|
| [C++] 1007번 벡터 매칭 (0) | 2024.12.27 |
| [Python] 9612번 Maximum Word Frequency (0) | 2024.11.30 |
| [Python] 8094번 Canoes (0) | 2024.11.29 |
| [Python] 32823번 채굴권 분할 (0) | 2024.11.28 |