https://www.acmicpc.net/problem/31529
24/03/09
맷코 컵의 검수진으로 검수를 했던 문제 중 하나이다. 단순한 기하학 문제이다.
문제 접근 방식:
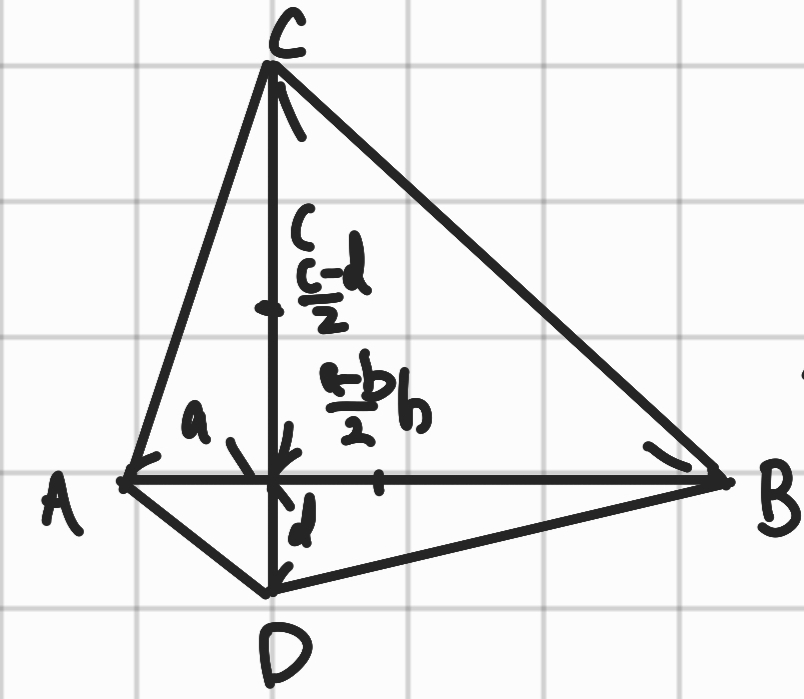
원점에서 $A$까지 떨어진 거리를 $a$, 원점에서 $B$까지 떨어진 거리를 $b$, 마찬가지로, $c, d$가 있다고 하자.
그러면 $\overline{AC}^{2} + \overline{BD}^{2} = X = a^2 + b^2 + c^2 + d^2$으로 나타낼 수 있다.
마찬가지로, $Y = (a+b)^2 + (c+d)^2 = a^2 + b^2 + c^2 + d^2 + 2ab + 2cd$으로 표현할 수 있다.
$M$과 $N$의 좌표는 $\frac{a-b}{2}$와 $\frac{c-d}{2}$이므로, $\overline{MN}^{2}$을 계산하면 다음과 같다.
$$\begin{align} \overline{MN}^2 &= \left( \frac{a-b}{2} \right) ^2 + \left( \frac{c-d}{2} \right) ^2 \\ &= \frac{1}{4} [ (a-b)^2 + (c-d)^2] \\ &= \frac{1}{4} [a^2 + b^2 + c^2 + d^2 - 2ab - 2cd] \\ &= \frac{1}{4} [Y-2(Y-X)] \\ &= \frac{1}{4}[2X-Y] = W\end{align}$$
이때, $Y-X = 2ab + 2cd$이므로, $Y \geq X$가 성립해야 하며, 길이의 제곱은 $0$보다 크거나 같아야 하므로 $2X \geq Y$가 성립해야 한다.
따라서, 이를 어긴다면 $-1$을 출력하도록 하면 된다.
저 조건을 만족한다면 위의 식으로 구한 $W$값에 $2024$를 곱한 값을 구하여 출력하면 된다.
$2024\cdot W$로 가능한 값이 여러 개 존재하는 경우는 없다. 식을 잘 정리하면 저 문장은 낚시라는 사실을 알 수 있다.
아래는 내가 위의 접근 방식과 같이 작성한 파이썬 코드이다. 더보기를 누르면 확인할 수 있다.
# 2024년에는 혼자가 아니길
import sys
input = sys.stdin.readline
X, Y = map(int, input().split())
if Y < X or 2*X < Y:
print(-1)
else:
print(1012*X - 506*Y)'알고리즘 > 백준 문제 풀이' 카테고리의 다른 글
| [Python] 2600번 구슬게임 (0) | 2024.05.18 |
|---|---|
| [Python] 2118번 두 개의 탑 (0) | 2024.05.17 |
| [Python] 31531번 공들의 리듬게임 (0) | 2024.05.15 |
| [Python] 1160번 Random Number Generator (0) | 2024.05.14 |
| [Python] 30912번 위잉위잉 (0) | 2024.05.13 |

