https://www.acmicpc.net/problem/1364
1364번: 울타리 치기
육각형 블록들로 이루어진 RPG 세계가 있다. 그 세계에 나라를 세우려고 하는 군주 캐릭터 송유진은 일반 블록을 울타리 블록으로 바꿀 수 있는 아이템을 N개 가지고 있다. 유진이가 이 N개의 아
www.acmicpc.net
24/01/16
백준 그룹 연습 문제로 나왔던 문제 중 하나다. 수열의 규칙을 찾아서 이를 코드로 구현하면 된다.
문제 접근 방식:
수열의 규칙은 다음과 같이 찾았다.
먼저, $1$부터 $5$까지는 $1$부터 $5$그대로 나옴을 쉽게 확인할 수 있다.
$6$부터는 조금 다르게 나오는데, 그 이유는 육각형 울타리가 둘러싸는 면적이 생기기 때문이다.

$7$의 경우는 다음과 같이 나온다.
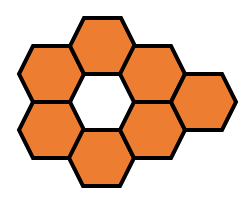
$8$의 경우는 다음과 같이 나온다.
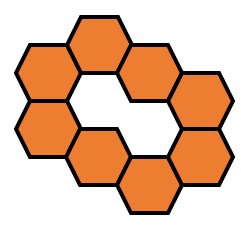
$9$의 경우는 다음과 같이 나온다.

$10$의 경우는 다음과 같이 나온다.
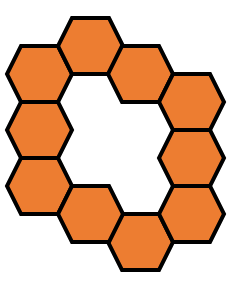
$11$의 경우는 다음과 같이 나온다.

$12$의 경우는 다음과 같이 나온다.

$13$의 경우는 다음과 같이 나온다.

$14$의 경우는 다음과 같이 나온다.
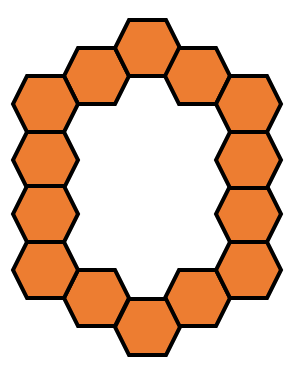
$15$의 경우는 다음과 같이 나온다.
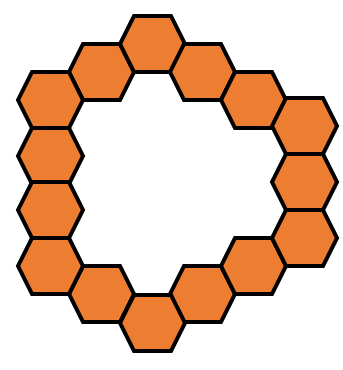
각 울타리 개수마다 나올 수 있는 최대의 답을 $15$까지 나열하면 다음과 같다.
| 울타리 개수 | 영역 | 울타리 개수 | 영역 | 울타리 개수 | 영역 |
| 1 | 1 | 6 | 7 | 11 | 16 |
| 2 | 2 | 7 | 8 | 12 | 19 |
| 3 | 3 | 8 | 10 | 13 | 21 |
| 4 | 4 | 9 | 12 | 14 | 24 |
| 5 | 5 | 10 | 14 | 15 | 27 |
여기서 우리는 $6$의 배수들에 주목할 필요가 있다.
$6$의 경우와 $12$의 경우를 보면 알 수 있듯이, 저 경우에서는 육각형 모양으로 둘러싸는 것이 최대의 영역을 만들어 낸다.
그리고 $6$의 배수들만이 저렇게 울타리의 모양을 육각형 모양으로 만들 수 있다는 사실을 알고 있다.
나는 이 수열에서 숫자가 증가하는 규칙을 살펴보았다.
처음에는 $1$씩 증가하다가, $6$의 배수로 넘어갈 때, 그보다 하나가 더 큰 $2$만큼 증가하고, 이후 다시 $1$씩 증가한 후에, $2$씩 증가함을 확인할 수 있었다.
마찬가지로, $12$가 될때 $3$만큼 증가하고 이후 다시 $2$만큼 증가했다가 이후에 계속 $3$만큼 증가함을 확인할 수 있었다.
정리하면 다음과 같다.
$6$의 배수인 경우는 이전 증가량보다 $1$만큼 더 큰 증가량을 지닌다.
$6$의 배수보다 하나가 큰 수는 이전 증가량보다 $1$만큼 작은 증가량을 지닌다.
$6$의 배수보다 둘이 큰 수는 이전 증가량보다 $1$만큼 더 큰 증가량을 지닌다.
따라서 이를 그대로 구현했다.
일반항은 따로 생각해보지 않아서 잘 모르겠다.
기여 창에서는 OEIS에 나와있다고 하는데, 왜 이 수열이 나오는지는 잘 모르겠다.
아래는 내가 위의 접근 방식과 같이 작성한 파이썬 코드이다. 더보기를 누르면 확인할 수 있다.
# 1364번 울타리 치기
# 수학
DP = [0 for _ in range(1_000_000 + 1)]
plus = 1
def is_six(num):
if num == 1:
return True
return not (num % 6)
DP[1], DP[2], DP[3] = 1, 2, 3
for i in range(4, 1_000_000+1):
if is_six(i):
DP[i] = DP[i-1] + plus + 1
elif is_six(i-1):
DP[i] = DP[i-1] + plus
elif is_six(i-2):
plus += 1
DP[i] = DP[i-1] + plus
else:
DP[i] = DP[i-1] + plus
print(DP[int(input())])'알고리즘 > 백준 문제 풀이' 카테고리의 다른 글
| [Python] 2290번 LCD Test (0) | 2024.02.06 |
|---|---|
| [Python] 2676번 라스칼 삼각형 (0) | 2024.02.06 |
| [Python] 2084번 차수열 (0) | 2024.01.23 |
| [Python] 1038번 감소하는 수 (0) | 2024.01.23 |
| [Python] 31229번 또 수열 문제야 (0) | 2024.01.22 |