2023.07.28 - [수학 공부 기록] - [딥러닝의 수학] 1. Introduction
[딥러닝의 수학] 1. Introduction
딥러닝 시리즈의 첫 번째 글입니다. 이 글은 고려대학교 수학과 오승상 교수님의 딥러닝 강좌를 참고자료로 하여 쓰임을 밝힙니다. 또한, 이 글의 목적은 이 강좌를 듣고 저의 개인적인 복습용
lighter.tistory.com
딥러닝 시리즈의 두 번째 글입니다. 이 글은 고려대학교 수학과 오승상 교수님의 딥러닝 강좌를 참고자료로 하여 쓰임을 밝힙니다. 또한, 이 글의 목적은 이 강좌를 듣고 저의 개인적인 복습용으로 요약하여 작성하는 것임을 밝힙니다. 자세한 내용을 알고 싶으시다면 아래 링크를 참고해 주세요.
https://youtube.com/playlist?list=PLvbUC2Zh5oJvByu9KL82bswYT2IKf0K1M
오승상 딥러닝 Deep Learning
고려대학교 오승상 교수의 Deep Learning 강의 입니다. (자료) https://sites.google.com/view/seungsangoh
www.youtube.com
이 글과 이후 글에서는 딥러닝의 핵심 개념 중 하나인 Deep Neural Network(DNN)에 대해 다룰 것입니다.
특히, 딥러닝에 대한 간략한 모티베이션을 시작으로 하여, 딥러닝의 가장 기초가 되는 단위인 퍼셉트론(뉴런)이 어떻게 작동하는지 알아보고 이를 토대로 하여 이전에 다루었던 Programming과 Learning의 차이점을 알아볼 것입니다.
이후 딥러닝 역사에서 중요한 문제 중 하나인 XOR Problem에 대해 간략하게 알아보고, 이를 극복하기 위한 방법 중 하나로 나온 Multilayer Perceptron Architecture에 대해 알아보도록 하겠습니다.
딥러닝에 대한 간략한 모티베이션을 가져가봅시다.
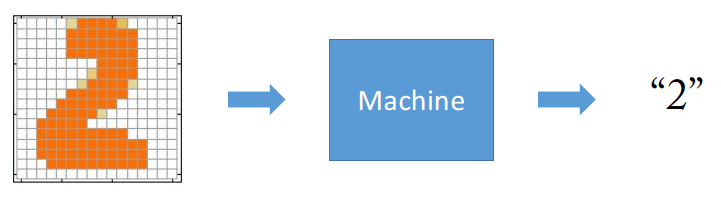
위에 있는 손글씨 2를 기계를 통해 2라는 글자로 인식시키고 싶어합니다.
이 과정을 딥러닝의 과정으로 이해해 봅시다.
사람은 이 손글씨를 쉽게 알아들을 수 있지만, 컴퓨터에게는 쉽게 알아들을 수 없기에 다음과 같은 과정을 거쳐서 알아듣게 만듭니다.
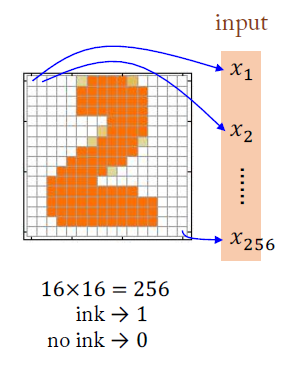
예를 들어, 이 손글씨는 총 $16 \times 16 = 256$개의 픽셀로 이루어져 있으므로, 각 픽셀이 켜져 있나 꺼져있나를 $0$과 $1$로 표시하여 총 $256$크기의 input vector로 하나의 이미지를 나타낼 수 있을 것입니다.
우리는 이 vector를 기계에 넣습니다.

손글씨는 총 0~9까지 10개의 숫자들을 인식해야 하는 상황에 있으므로, output vector의 크기는 10이라고 이야기할 수 있습니다.
또한, 각 vector의 원소는 $0$이나 $1$로만 나오는 것이 아니라, $0$과 $1$사이의 일정 확률 값으로 나오게 됩니다.
즉, 각 원소($\hat{y}_1, \hat{y}_2, ... \hat{y}_{10}$)가 각 digit의 신뢰성(confidence)을 의미합니다.

즉, 요약하자면 다음 그림과 같습니다.
이 예시에서는 Machine을 일종의 $f : \mathbb{R}^{256} \rightarrow \mathbb{R}^{10}$로 바라볼 수 있습니다.
DL에서는 이 $f$가 Neural Network로 표현이 됩니다.
Perceptron은 뉴런의 기능을 본떠 만든 일종의 인공 신경망입니다.
이를 알기 위해서는 실제 뉴런의 작동 기능을 봐야 합니다.
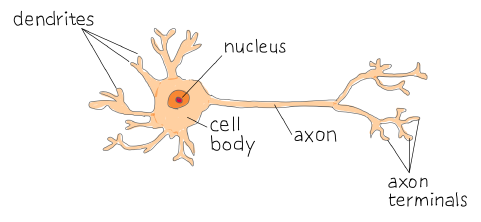
다음과 같이 뉴런은 Dendrites에서 여러 다양한 자극들을 받는데, 상황에 따라 이 자극들은 Axon을 타고 끝까지 전달될 수도 있고, 전달되지 않을 수도 있습니다.
일종의 임계치(Threshold)를 넘기게 되면 뉴런은 이를 진정한 "자극"으로 인식하여 전달하게 됩니다.
마치 $0$과 $1$이 있는 스위치를 누르는 것처럼, 뉴런 또한 다양한 자극들이 임계치 이하로 들어온다면 그 자극들은 전달하지 않고($0$), 임계치를 넘긴다면 그 자극은 $1$로 전달하게 됩니다.(Activation)
인공 신경망도 이와 마찬가지로, 입력을 받는 부분이 존재하고, 이 입력이 얼마큼 중요한지를 나타내는 가중치(Weight)가 존재하며, 이들을 모두 합하고 편향(Bias)을 더하여, 최종적으로 전달이 되냐 되지 않냐의 여부를 알려주는 Activation function을 거칩니다.

입력 벡터 $x = (x_1, x_2,... , x_k)$가 각각의 Weight($w_i$)들에 곱해지고, 그 값들과 bias $b$를 합친 값 $z = \sum {x_i w_i} + b$이 만들어집니다.
이 값(weighted sum) $z$는 activation function $\sigma$를 거치게 됩니다.
중요한 점은, $\sigma$는 뉴런처럼 전달이 되냐 안 되냐 처럼 $0$과 $1$로 구분되는 것이 아니라 nonlinear 하게 부드럽게 이어져 있어서, $0$과 $1$사이의 값으로 나온다는 사실입니다.(output vector $\hat{y}$)
주로 activation function에는 아래 그림과 같은 sigmoid함수를 사용하는데, 이에 대해서는 추후에 배웁니다.

여기서 Programming과 Learning의 차이점을 한번 되짚어 보도록 합시다.

이번엔 인공신경망을 다음과 같이 구성해서 $X$ and $Y$의 결괏값을 내보내는 걸 생각해 봅시다.
bias $b$값은 $1$이고, 각각의 weight값은 $1, 1, -2$입니다. 즉, $X + Y -2$를 아래와 같은 step function에 넣어서 activation을 시켰다고 해봅시다.
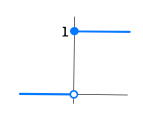
그러면 이 결괏값은 $X$ and $Y$의 결괏값과 동일한 결과를 내보냅니다.
마찬가지로, OR과 NOT 또한 아래와 같이 인공신경망의 형태로 만들 수 있습니다.

사실은 이런 경우를 우리가 인공 신경망이라고 부르지는 않습니다.
우리가 저 상황에 맞게 "미리" 가중치들을 정해주었기 때문입니다.
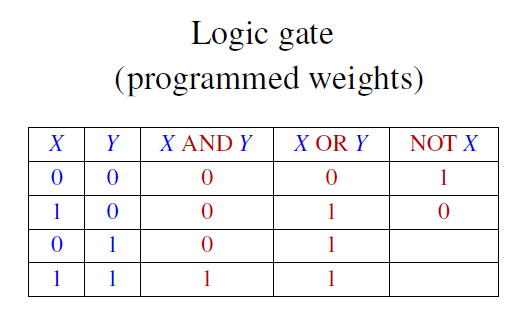
즉, weight들이 미리 programmed 되어있습니다.
또한, 지금은 $X$와 $Y$로만 해서 weight들을 구하기가 매우 쉬웠지만, 이러한 입력값들이 많아진다면 어떻게 해야 할까요?
여기서 Learning과 Programming의 다른 점이 나옵니다.

실제 신경망은 각 $x_i$별로 들어오는 $w_i$들이 매우 많기 때문에 우리가 직접 미리 정해줄 수 없습니다.
때문에 weight들의 값을 업데이트를 해주면서 바꿔줘야 합니다.
이러한 특성을 Learning이라고 이야기합니다.
또한, $0$과 $1$로만 나오는 것이 아니라 그 사이의 확률로 나옵니다.
이 또한 업데이트를 해주기 위한 장치라고 생각해 주면 됩니다.
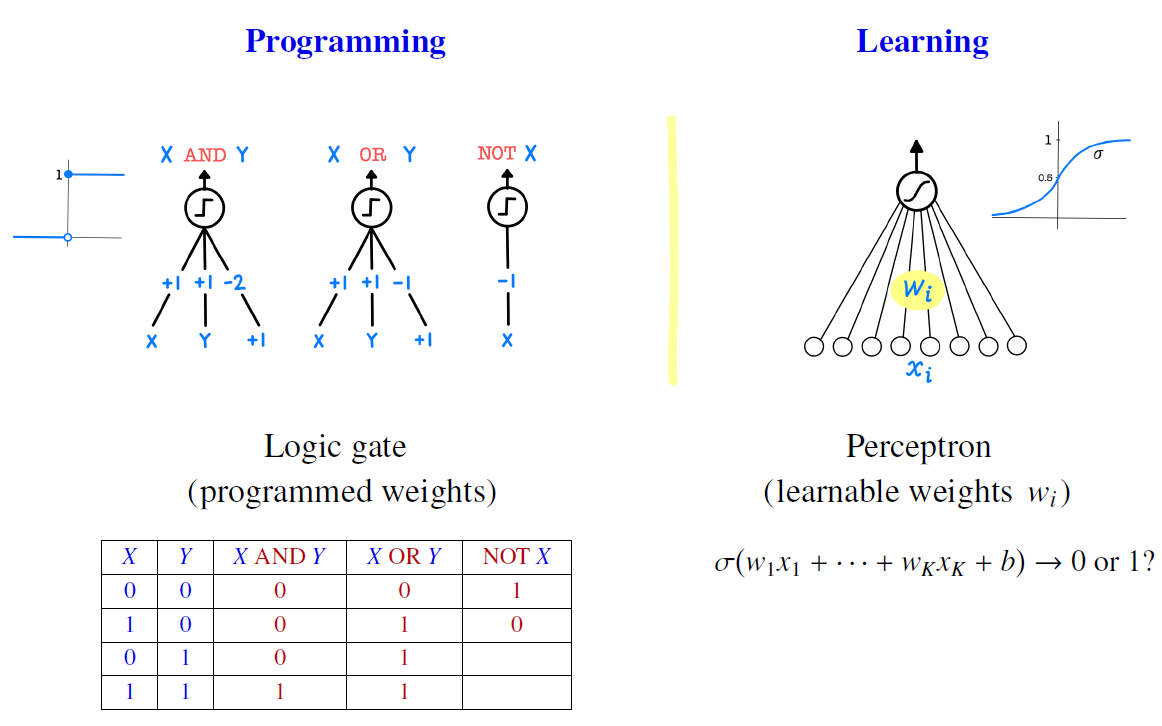
하지만 Perceptron 또한 한계가 존재했습니다.
그것은 AI에서 유명한 문제 중 하나인 XOR Problem입니다.
weighted sum $z$를 생각해 보면 linear 한 특성을 지니고 있다는 것을 우리는 알고 있습니다.
따라서 하나의 Perceptron은 데이터를 구분선 "하나"로 분리하는 것처럼 생각할 수 있습니다.

하지만, 이는 XOR의 특성을 지닌 데이터들(즉, not linear 한)은 위와 같이 구분선 하나로만 구분 지을 수 없습니다.
이는 근본적인 Perceptron의 한계입니다.
이를 해결하기 위해서는 Perceptron을 여러 개 도입하는 방법을 사용할 수 있습니다.(Multilayer Perceptron)

즉, 구분선을 여러 개 긋는 것이죠.
이 Perceptron을 여러 개 도입하면, 각각의 weight 또한 계산해야 되는 양이 많아져서 이를 효율적으로 계산해야 됩니다.
이 방법은 추후 Hinton이 1986년 Backpropagation이라는 방법을 고안하게 되면서 AI연구는 이 시기를 기점으로 발전하게 되었습니다.
Multilayer Perceptron Architecture은 다음과 같은 구조를 지닙니다.
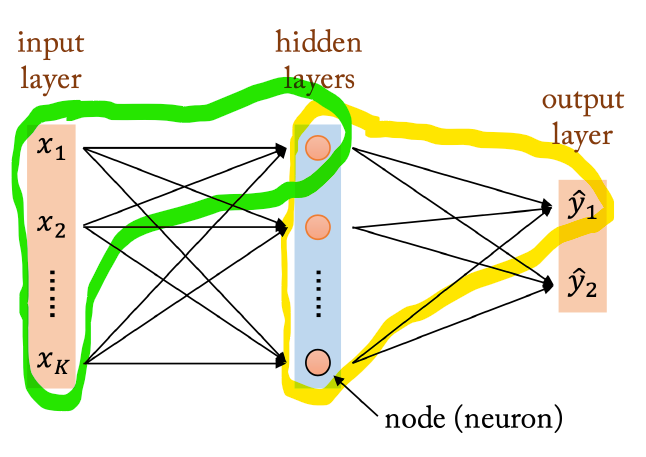
Input layer, Hidden layer, Output layer로 구분되며, 초록색으로 테두리를 쳐놓은 것이 하나의 Perceptron입니다.
즉, 여러 개의 Perceptron을 그림과 같이 병렬로 나열해 놓은 것을 Layer라고 부르는 것입니다.
이 Layer는 노란색으로 테두리를 쳐 둔 그림과 같이 또 다른 Layer의 한 곳에 연결이 됩니다.
이 또한 하나의 Perceptron으로 간주할 수 있습니다.
이처럼 Input layer를 제외한 모든 node들은 하나의 Perceptron의 끝부분에 해당됨을 알 수 있습니다.
또한, 각 Perceptron마다 weight들이 다릅니다.
병렬로 node들이 나열되어 있는 모습을 Layer라고 했는데, Layer의 개수가 많으면 많을수록 일반적으로 MLP의 성능 또한 좋아집니다.

위 그림처럼, 어떤 데이터를 구분하는 구분선으로 예시를 들었다면, Layer의 개수가 많아지면 많아질수록 그 구분하는 정확도 또한 증가함을 확인할 수 있습니다.
'공부 기록 > 딥러닝의 수학' 카테고리의 다른 글
| [딥러닝의 수학] 5. Stochastic Gradient Descent (0) | 2023.08.10 |
|---|---|
| [딥러닝의 수학] 4. Cost, Gradient Descent (0) | 2023.08.05 |
| [딥러닝의 수학] 3. DNN, Forward Pass (0) | 2023.07.31 |
| [딥러닝의 수학] 1. Introduction (2) | 2023.07.28 |


