https://www.acmicpc.net/problem/11668
24/05/12
기하학 + 그래프 이론 관련 문제이다.
좋은 문제인 것 같아서 풀이를 남겨보려고 한다.
문제 접근 방식:
문제에서 요구하고 있는 바를 정리해보자.
1. 파이프는 수원지와 도시를 잇는다.
2. 두 파이프는 서로 교차할 수 있으며, 한 교차점에는 세 파이프가 동시에 교차하지 않는다.
3. 교차점에는 이물질이 끼는데, 한 파이프에 로봇을 넣으면 그 파이프의 교차점을 모두 청소해 줌.
4. 로봇이 충돌하는 일을 방지하기 위해 교차점에는 오직 하나의 파이프에만 로봇이 있어야 함.
5. 어떤 파이프의 부분 집합을 잡아서 동시에 로봇을 투입했을 때, 두 로봇이 충돌하는 일이 없으면서 모든 교차점을 청소할 수 있는지를 판단해야 함.
6. 두 파이프의 교차점은 두 파이프의 끝 점이 될 수 있지만, 시작점(수원지)은 될 수 없음.
이 요구 사항을 예제 입력 1을 통해 확인해 보자.
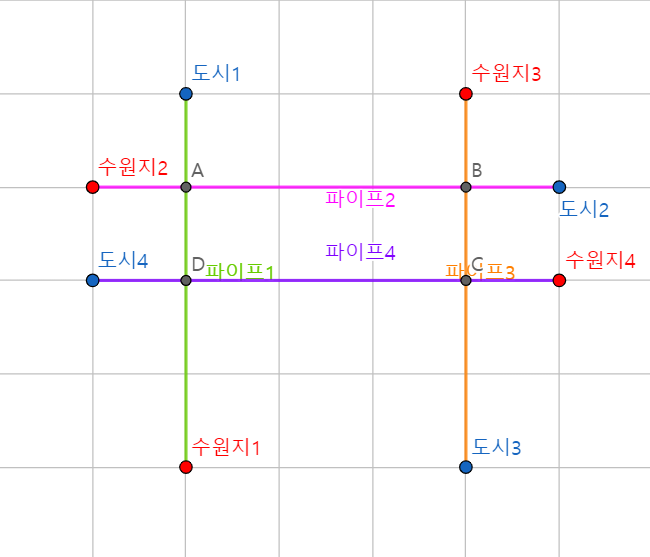
예제 입력 1을 그림으로 표현하면 다음과 같이 표시할 수 있다.

만약 여기서 파이프 1에 로봇을 넣는다고 한다면, 파이프 1의 교차점들인 B와 C의 이물질을 제거할 수 있지만, A의 이물질은 제거할 수 없다.
A의 이물질을 제거하기 위해서는 파이프 2나 파이프 3에 로봇을 넣어야 하는데, 이렇게 되면 파이프 1에 넣었던 로봇과 충돌하게 된다.
따라서, 어떻게 로봇을 넣는다고 해도, 모든 곳을 교차점을 청소하면서 로봇끼리 충돌할 수 없도록 만들 수 없다.
예제 입력 2를 그림을 통해 확인해보자.

이 경우, 수원지에서 파이프가 만나는 것은 교차점으로 간주를 하지 않는다고 했으므로, 교차점은 두 곳이 만들어진다.
파이프 3에 로봇을 넣는다면 모든 교차점을 청소할 수 있으므로 가능하다.
예제 입력 1과 예제 입력 2를 잘 살펴보면, 파이프마다 번호를 부여할 수 있고, 이 파이프가 서로 만나는 것을 간선이 이어진 상태라고 생각하여 하나의 그래프로 모델링 할 수 있음을 알 수 있다.
그렇게 모델링한 그래프가 홀수 길이의 사이클을 가지면 불가능하다는 사실을 관찰을 통해 알아낼 수 있다.
다음과 같은 또 다른 불가능한 예시를 확인해보자.

이 경우 A를 청소하기 위해서는 파이프 1이나 파이프 2 둘 중 하나의 파이프에 로봇을 넣어야 한다.
둘 중 한 곳에 넣었다고 하면, 예를 들어, 파이프 2에 로봇을 넣었다고 하면, 파이프 1이나 파이프 3에는 로봇을 넣을 수 없다.
그러면 E를 청소하기 위해 파이프 5에 로봇을 넣을 수 밖에 없고, 마찬가지로 C를 청소하기 위해 파이프 4에 로봇을 넣을 수 밖에 없다. 그러면 두 로봇이 충돌하므로 이는 불가능하다는 것을 알 수 있다.
예제 입력 1과 다음과 같은 불가능한 경우의 예시를 통해 알 수 있듯이, 모델링한 그래프가 홀수 길이의 사이클을 가진다면, 로봇끼리 어떻게든 만날 수 밖에 없다는 사실을 알 수 있다.
반면, 다음과 같이 짝수 길이의 사이클을 가지는 것은 별 문제가 되지 않는다. 이 예시의 경우, 파이프 2와 파이프 4를 택하면 된다.
따라서, 우리는 만나는 교점의 관계를 그래프로 표현한 뒤, 홀수 길이의 사이클이 존재한다면 불가능이라고 판정하면 충분하다.
그러면 홀수 길이의 사이클이 존재하는 것은 어떻게 판정할까?
이는 다음과 같은 명제를 통해 판별할 수 있다.
홀수 길이의 사이클을 가지지 않는 그래프는 이분 그래프와 동치이다.
이 명제의 증명은 다음과 같다.
증명)
1) 이분 그래프는 홀수 길이의 사이클을 가지지 않는다.
어떤 그래프 $G$가 이분 그래프라고 하자.
그러면 $G$의 정점 집합 $V$는 두 개의 정점 집합(Vertex set) $V_1, V_2$로 분할된다.
$V_1$에 속해 있는 어떠한 정점 $v$가 존재한다고 하자.
$v$에 연결되어 있는 간선들이 있어서, 사이클이 만들어 진다고 가정하자.
이분 그래프의 정의에 따라, 하나의 정점에서 다른 정점으로 갈 때마다, $V_1$에 속해있던 정점이라면 $V_2$로, $V_2$에 속해있던 정점이라면 $V_1$으로 갈 것이다.
따라서, $v$로 시작하여 $v$로 도착하는 사이클은 짝수 길이만 만들어질 뿐, 홀수 길이의 사이클이 만들어지지 못함을 확인할 수 있다.
2) 홀수 길이의 사이클을 가지지 않는 그래프는 이분 그래프이다.
어떤 그래프 $G$가 홀수 길이의 사이클을 가지지 않는다고 하자.
$G$에 있는 정점 $v_0$를 임의로 잡고, 다음과 같이 정점들을 두 가지로 분류해보자.
$V_1 = v_0$에서 $v$로 가는 가장 짧은 경로의 길이가 짝수 길이인 $v$들의 집합.
$V_2 = v_0$에서 $v$로 가는 가장 짧은 경로의 길이가 홀수 길이인 $v$들의 집합.
우리는 이 $V_1, V_2$가 이분 그래프의 정의에 부합하는지 확인하면 된다.
즉, $V_1$에 속해 있는 두 정점이나 $V_2$에 속해 있는 두 정점 사이에 간선이 없음을 확인하면 된다.
만약에, $V_1$에 속해 있는 어떠한 두 정점 사이에 간선이 존재한다고 해보자.(귀류법)
이 두 정점을 각각 $v_1, v_2$라고 해보자.
그렇다면, $v_0$에서 $v_1$으로 가서 $v_1$에서 $v_2$로 가고, $v_2$에서 다시 $v_0$로 돌아오는 경로는 닫힌 경로를 형성한다. 이 닫힌 경로는 홀수 길이를 가진다.
닫힌 경로에서 중복으로 지나가는 간선은 짝수 번 지나가고, 이를 경로에서 제거한다면 홀수 길이의 사이클을 얻을 수 있다.
이는 어떤 그래프 $G$가 홀수 길이의 사이클을 가지지 않는다고 한 것과 모순이므로, $V_1$에 속해 있는 정점끼리는 서로 간선이 존재하지 않는다.
마찬가지로, $V_2$에 속해 있는 정점끼리는 서로 간선이 존재하지 않는다.
따라서, 이 명제를 활용하여 이분 그래프임을 판정하고, 만약 이분 그래프가 아니라면 홀수 길이의 사이클을 가지는 그래프이기 때문에 불가능하다고 판별하면 된다.
이분 그래프라면 가능하다고 판별하면 된다.
구현 시 유의할 점은 선분 교차 판정이 살짝 다르다는 점이다. 수원지가 겹치는 경우는 선분이 교차한 경우로 판별하지 않지만, 도시가 겹치는 경우 선분이 교차한 경우로 판별한다.
이분 그래프 판별은 BFS나 DFS등으로 쉽게 판별 가능하며, 이는 이 문제를 풀 정도의 수준이라면 따로 설명하지 않아도 알 수 있을 것 같아, 설명은 생략하도록 하겠다.
아래는 내가 위의 접근 방식과 같이 작성한 파이썬 코드이다. 더보기를 누르면 확인할 수 있다.
# 11668번 파이프 청소
# 기하, 선분 교차 판정, 이분그래프
'''
접근 방법:
만나는 교점의 관계를 그래프로 표현한 뒤,
odd-cycle이 존재하면 불가능으로 판정한다.
'''
import sys
input = sys.stdin.readline
from collections import deque
def CCW(P1, P2, P3):
A, B = (P2[0]-P1[0], P2[1]-P1[1]), (P3[0]-P2[0], P3[1]-P2[1])
K = A[0]*B[1] - A[1]*B[0]
if K > 0: return 1
elif K == 0: return 0
else: return -1
def is_meet(line1, line2):
S1, E1 = line1
S2, E2 = line2
if E1 == E2: return True # 파이프의 끝점이 겹치는 경우
if S1 == S2: return False # 수원지가 겹치는 경우
# 선분이 평행하게 만나지 않음에 유의하자.
if CCW(S1, E1, E2)*CCW(S1, E1, S2) < 0 and CCW(S2, E2, S1)*CCW(S2, E2, E1) < 0:
return True
else:
return False
def BFS(start, visited, graph):
queue = deque()
queue.append(start)
visited[start] = 1
while queue:
now = queue.popleft()
color = 0
if visited[now] == 1:
color = 2
elif visited[now] == 2:
color = 1
for near in graph[now]:
if visited[near] == 0:
visited[near] = color
queue.append(near)
return visited
def is_bipartite(graph):
visited = [0 for _ in range(len(graph))]
for node in range(len(graph)):
if visited[node] == 0:
visited = BFS(node, visited, graph)
for node in range(len(graph)):
S = set(visited[i] for i in graph[node])
if visited[node] == 1 and 1 in S:
return False
if visited[node] == 2 and 2 in S:
return False
return True
# 수원지의 개수, 파이프의 개수
W, P = map(int, input().split())
# 수원지 입력
sources = []
for _ in range(W):
x, y = map(int, input().split())
sources.append((x, y))
# 선분들 입력받기
pipes = []
for _ in range(P):
s, x, y = map(int, input().split())
pipes.append((sources[s-1], (x,y)))
# 선분 교차 관계를 나타내는 그래프
G = [[] for _ in range(P)]
for i in range(P-1):
for j in range(i+1, P):
if is_meet(pipes[i], pipes[j]):
G[i].append(j)
G[j].append(i)
if is_bipartite(G):
print('possible')
else:
print('impossible')'알고리즘 > 백준 문제 풀이' 카테고리의 다른 글
| [Python] 1160번 Random Number Generator (0) | 2024.05.14 |
|---|---|
| [Python] 30912번 위잉위잉 (0) | 2024.05.13 |
| [Python] 20302번 민트 초코 (0) | 2024.04.19 |
| [Python] 5069번 미로에 갇힌 상근 (0) | 2024.04.19 |
| [Python] 31532번 선형 회귀는 너무 쉬워 3 (0) | 2024.04.18 |