https://www.acmicpc.net/problem/27306
27306번: DAGame
첫 번째 줄에 노드의 개수를 나타내는 정수 $N$ ($2 \le N \leq 500$), 간선의 개수를 나타내는 정수 $M$ ($1 \leq M \leq 100\,000$)이 주어진다. 두 번째 줄 부터 $M$개의 줄에 서로 다른 두 정수 $p$, $q$ ($1 \leq p$
www.acmicpc.net
23/05/03
스프라그-그런디 정리에 대한 이해도가 있어야 해결할 수 있는 문제다.
몇몇 사람들은 스프라그-그런디 정리의 문제를 풀 때 결과만 외우고 그냥 XOR계산만 적용해서 문제를 푸는 경우가 좀 있다고 생각한다.
나도 스프라그-그런디 정리를 적용한 문제를 처음 풀었을 때, 이해 없이 결과만 받아들이고 문제를 풀었던 경험이 있었기에, 이 문제의 해설을 통해 스프라그-그런디 정리에 대한 이해도를 더욱 높이고자 한다.
문제 접근 방식:
핵심은 결국 스프라그-그런디 정리에서 나오는 게임들은 전부 DAG(사이클이 없는 방향 그래프)로 생각할 수 있다는 것이다.(물론 엄밀하지는 않다. 하지만, 사이클이 있다면 그런디 수로 풀기가 힘들다. 그런디 수를 구할 때, 재귀적으로 구하는데, 이를 생각해 보면 사이클이 있다면 무한루프가 난다...)
스프라그-그런디 정리를 일반적으로 입문할 때, 각 게임판의 "상황"을 하나의 "그런디 수"로 치환할 수 있다는 이야기를 많이 들었을 것이다.
편의상 $A$라는 게임판의 "상황"이 있고, $B$, $C$, $D$라는 게임판의 "상황"에서 어떤 한 사람이 "행동"을 해서 $A$라는 게임판의 "상황"으로 갈 수 있다고 해보자.
우리는 $A$라는 게임판의 "상황"을 하나의 "노드"라고 간주할 수 있고, 마찬가지로, $B$, $C$, $D$ 또한 하나의 "노드"라고 간주할 수 있다.
즉, $B$, $C$, $D$라는 게임판의 "상황"에서 어떤 행동으로 인해 $A$라는 게임판의 "상황"이 만들어 졌다는 것의 의미는 $B$, $C$, $D$라는 노드에서 $A$라는 노드로 이동했다는 의미로 해석할 수 있다.
즉, 내가 어떠한 행동을 한다는 것은 "노드와 노드 사이의 이동"으로 간주할 수 있다.
당연하게도, 이렇게 게임판들의 "상황"에 대한 모임들이 있고, 행동을 해서 게임판의 상황이 바뀌는 "정보"들이 있다면, 우리는 각 게임판의 "상황"을 "노드"로, 행동을 해서 게임판의 상황이 바뀌는 "정보"들을 노드와 노드를 잇는 "간선"으로 생각할 수 있다.
첫 번째 예시로 이런 상황을 들어보자.
처음에 어떤 자연수 $N$이 적혀 있다. 플레이어가 할 수 있는 행동은 $1$을 제외한 $N$의 진약수 중 하나를 선택하고, 쓰여 있는 $N$을 지우고 그 진약수를 다시 적는 것이다.
이를 반복하다가, 더 이상 행동을 할 수 없는 사람이 지는 게임이 있다고 해보자.
(물론 이 게임은 스프라그-그런디 정리로 굳이 접근하지 않아도 되지만, 이해를 돕기 위해 넣었다.)
https://www.acmicpc.net/problem/16894
16894번: 약수 게임
구사과와 큐브러버는 약수 게임을 하려고 한다. 약수 게임은 종이에 정수를 적으면서 진행하고, 두 사람은 턴을 번갈아 가진다. 가장 처음에 종이에는 정수 N이 적혀있다. 각자의 턴이 돌아올
www.acmicpc.net
그렇다면 우리는 $1$부터 $10$까지의 상황들을 다음과 같은 그래프처럼 묘사할 수 있다.
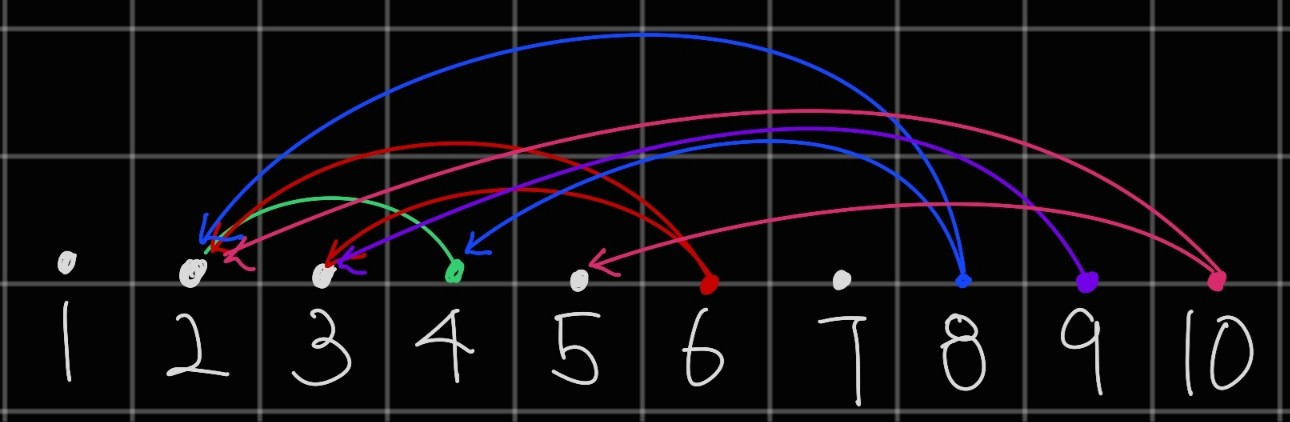
만약 위의 "약수 게임"을 여러 개 "동시에" 진행한다면, XOR을 써야 하는 상황이 생길 수 있다.
두 번째 예시로, 다음과 같은 게임판에서 말을 한 칸씩 움직이는 게임이 있다고 해보자.
이 또한 더 이상 말을 움직이지 못하는 플레이어가 진다.
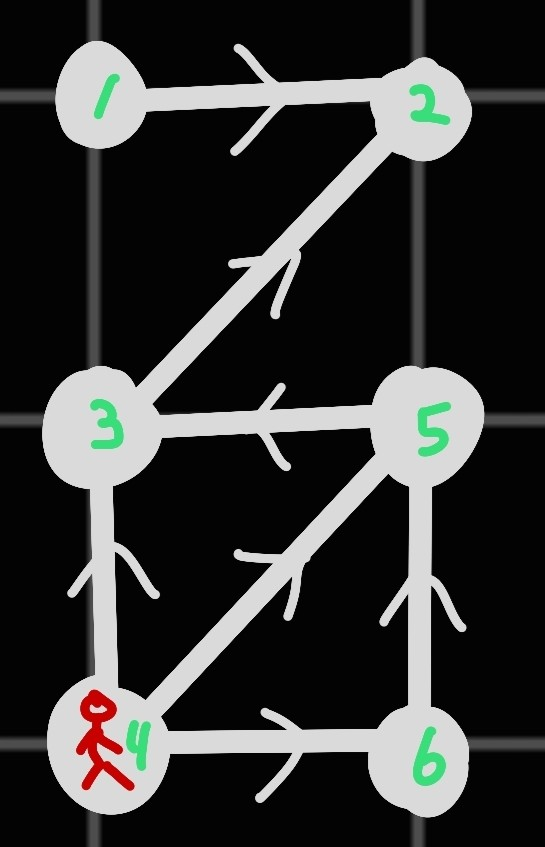
$1$번 노드부터 $6$번 노드까지 있고, 다음과 같이 간선이 주어져 있는 상황이다.
말은 $4$번 노드에서 시작하여 다른 노드로 움직일 것이다.
누가 이길까 곰곰히 생각해 보면 선공이 이긴다는 사실을 알 수 있다.
그런데, 이 상황을 확장해서, 말을 여러 개 놓고 한다면 어떻게 할까?
그렇다면, 여러 개의 게임을 동시에 진행하는 것이므로, 하나의 게임판에 대한 그런디 수를 모두 구해봐야 한다.
이 게임판의 경우, 각 노드별로 말이 놓여, 총 6개의 게임판의 "상황"을 생각해 볼 수 있다.
$2$번 노드에 말이 있으면 더 이상 진행할 수 없으므로, $2$번 노드에 말이 있는 게임판의 "상황"에 대한 그런디 수는 $0$이 된다.
$1$번 노드에 말이 있다면, 우리는 그래프에서 볼 수 있듯, $2$번 노드로 말을 옮길 수 있으므로(즉, $2$번 노드에 말이 있는 게임판의 "상황"으로 갈 수 있으므로), $1$번 노드에 말이 있는 게임판의 "상황"에 대한 그런디 수는 $mex(0) = 1$가 된다.
$3$번 노드에 말이 있다면, $2$번 노드로 말을 옮길 수 있으므로, $3$번 노드에 말이 있는 게임판의 "상황"에 대한 그런디 수는 $mex(0) = 1$가 된다.
$5$번 노드에 말이 있다면, $3$번 노드로 말을 옮길 수 있으므로, $5$번 노드에 말이 있는 게임판의 "상황"에 대한 그런디 수는 $mex(1) = 0$이 된다.
$6$번 노드에 말이 있다면, $5$번 노드로 말을 옮길 수 있으므로, $6$번 노드에 말이 있는 게임판의 "상황"에 대한 그런디 수는 $mex(0) = 1$이 된다.
마지막으로, $4$번 노드에 말이 있다면, $3$번 노드, $5$번 노드, $6$번 노드로 말을 옮길 수 있다.
즉, $3$번 노드에 말이 있는 게임판의 상황, $5$번 노드에 말이 있는 게임판의 상황, $6$번 노드에 말이 있는 게임판의 상황을 모두 만들 수 있다는 것이므로, $4$번 노드에 말이 있는 게임판의 "상황"에 대한 그런디 수는 $mex(1, 0, 1) = 2$가 된다.
이를 참고해서 말이 여러 개 있을 때의 문제를 해결할 수 있다.
위의 두 개의 예시를 통해, 게임판의 특정 "상황"을 "노드"로, 한 게임판에서 어떤 동작을 통해 특정 게임판들을 만드는 행위를 "노드와 노드 사이의 이동"이라고 이해를 했다면, 스프라그-그런디에 대한 이해도가 높아진 것이다.
그렇다면, 이를 통해 문제를 한 번 이해해 보자.
일단 색깔이 서로 다른 것끼리는 영향을 주지 않는다고 했으므로, 색깔이 다른 것끼리는 서로 별개의 게임판, 즉, XOR을 해야 한다는 인식이 있어야 할 것이다.
이 문제에서 독특한 점은, 위의 두 번째 예시를 확장하여, 색깔이 같은 것이 최대 2개까지 있고, 만나면 서로 "업혀서" 같이 움직인다는 점이다.
그러면, 말이 하나 있는 경우를 통해 말이 두 개 있는 경우에 대한 그런디 수를 어떻게 구할까?
이를 생각하는 아이디어의 핵심은 역설적으로 "말이 하나 있는 경우"와, "말이 두 개 있는 경우"는 본질적으로 크게 다르지 않다는 점이다.
왜냐하면, "특정 노드에 말이 하나 있는 경우"는 두 개의 말이 "동시에 한 곳에 있는 경우"와 같기 때문이다.
만나면 "무조건" 업혀서 "같이" 가기 때문에, 그냥 "말이 하나 있는 경우"와 "말이 두 개 있는 경우"를 분리해서 생각할 필요가 없다.
예를 들어, 아래의 그림을 보자.

이런 경우, $5$번 노드에 놓인 두 개의 말은 같이 움직이므로 하나의 말로 생각할 수 있다.
그래서 그냥 그런디 수를 두 번째 예시처럼 구하면 그만이다.
그렇다면 따로 있는 경우는 어떻게 구해야 할까?
편의상 말이 $m$번 노드와 $n$번 노드에 있을 때의 게임판의 "상황"에 대한 그런디 수를 $grundy(m, n)$이라고 표기하자.

우리는 $1$번 노드의 말을 $2$번 노드 또는 $5$번 노드로 옮길 수 있다.
혹은, $5$번 노드의 말을 $6$번 노드 또는 $4$번 노드로 옮길 수 있다.
다시 말하자면, 이 상황에서 게임판의 상황을 다음과 같이 4가지 상황으로 바꿀 수 있다는 것이다.
1. $2$번 노드와 $5$번 노드에 말이 놓여있는 게임판의 상황($grundy(2, 5)$)
2. $5$번 노드와 $5$번 노드에 말이 놓여있는 게임판의 상황($grundy(5, 5)$)
3. $1$번 노드와 $4$번 노드에 말이 놓여있는 게임판의 상황($grundy(1, 4)$)
4. $1$번 노드와 $6$번 노드에 말이 놓여있는 게임판의 상황($grundy(1, 6)$)
따라서, 위의 그런디 수 표기법에 따르면, $grundy(1, 5)$의 값은 $mex(grundy(2, 5), grundy(5, 5), grundy(1, 4), grundy(1, 6))$이 된다.
그러면 $grundy(2, 5)$는 어떻게 구할까?
그건 그냥 재귀적으로 구하면 끝이다.
우린 이미 $grundy(5, 5)$의 값을 알고 있다!
위에서 $grundy(1, 1)$부터 $grundy(7, 7)$까지는 모두 말이 하나 있는 경우랑 별반 다르지 않으므로, 그냥 위에서 했던 예시처럼 똑같이 재귀적으로 미리 구해둔 후에, 이를 통해 일반적인 $grundy(m, n)$을 재귀적으로 구해주면 끝이다.
구현은 각자 알아서 해보길 바란다.
나의 경우, DFS로 구현했지만 몇몇 사람들의 경우 위상정렬을 통해 구현한 사람도 있었다.
아래는 내가 위의 접근 방식과 같이 작성한 파이썬 코드이다. 더 보기를 누르면 확인할 수 있다.
# 27306번 DAGame
# 게임 이론, 그래프 이론, 스프라그-그런디 정리, DFS
import sys
input = sys.stdin.readline
def mex(S):
for num, i in zip(sorted(S), range(len(S))):
if num != i:
return i
return len(S)
# 말 1개 있을 때의 nodegrundy를 구하는 함수
def determine_nodegrundy1(node):
if graph[node] == []:
grundy[node][node] = 0
return grundy[node][node]
else:
S = set()
for near_node in graph[node]:
if grundy[near_node][near_node] == -1:
determine_nodegrundy1(near_node)
S.add(grundy[near_node][near_node])
grundy[node][node] = mex(S)
return grundy[node][node]
# 말 2개 있을 때의 nodegrundy를 구하는 함수
def determine_nodegrundy2(node1, node2): # 입력은 항상 node1 < node2로 주어진다.
if graph[node1] == []:
grundy[node1][node2] = grundy[node2][node2]
return grundy[node1][node2]
elif graph[node2] == []:
grundy[node1][node2] = grundy[node1][node1]
return grundy[node1][node2]
else:
S = set()
for near_node in graph[node1]:
if near_node > node2:
if grundy[node2][near_node] == -1:
determine_nodegrundy2(node2, near_node)
S.add(grundy[node2][near_node])
else:
if grundy[near_node][node2] == -1:
determine_nodegrundy2(near_node, node2)
S.add(grundy[near_node][node2])
for near_node in graph[node2]:
if near_node > node1:
if grundy[node1][near_node] == -1:
determine_nodegrundy2(node1, near_node)
S.add(grundy[node1][near_node])
else:
if grundy[near_node][node1] == -1:
determine_nodegrundy2(near_node, node1)
S.add(grundy[near_node][node1])
grundy[node1][node2] = mex(S)
return grundy[node1][node2]
N, M = map(int, input().rstrip().split()) # number of nodes, number of edges
grundy = [[-1 for _ in range(N)] for _ in range(N)]
graph = [[] for _ in range(N)]
for _ in range(M):
p, q = map(lambda x: int(x)-1, input().rstrip().split())
if q in graph[p]:
pass
else:
graph[p].append(q)
for i in range(N):
if grundy[i][i] == -1:
determine_nodegrundy1(i)
for node1 in range(N-1):
for node2 in range(node1+1, N):
if grundy[node1][node2] == -1:
determine_nodegrundy2(node1, node2)
K = int(input())
stones = [[-1 for _ in range(N)] for _ in range(2)]
for _ in range(K):
v, c = map(lambda x: int(x)-1, input().rstrip().split())
if stones[0][c] == -1:
stones[0][c] = v
else:
stones[1][c] = v
total = 0
for c in range(N):
if stones[0][c] == -1:
continue
elif stones[1][c] == -1:
v = stones[0][c]
total ^= grundy[v][v]
else:
v1, v2 = stones[0][c], stones[1][c]
v1, v2 = min(v1, v2), max(v1, v2)
total ^= grundy[v1][v2]
print('Young' if total else 'Cheol')'알고리즘 > 백준 문제 풀이' 카테고리의 다른 글
| [Python] 19114번 Master Zhu and Candies (증명 추가 필요) (0) | 2023.05.17 |
|---|---|
| [Python] 스프라그-그런디 정리 활용 문제 모음 (0) | 2023.05.17 |
| [Python] 9066번 금고 (0) | 2023.03.21 |
| [Python] 9718번 Matrix Transformation (0) | 2023.03.14 |
| [Python] 2758번 로또 (0) | 2023.03.13 |