https://www.acmicpc.net/problem/11729
11729번: 하노이 탑 이동 순서
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로
www.acmicpc.net
22/11/25
전형적인 웰 노운 재귀 문제이다. 근데 솔직히 나는 사람들이 웰 노운 문제라면서 내려치기 하는 거 별로 안 좋아한다.
이 문제는 하노이 탑의 움직임이 어떻게 분할되는가에 집중하면 재귀적으로 쉽게 해결할 수 있는 문제이다.
문제 접근 방식:
하노이 탑의 움직임이 어떻게 분할되는지 한번 그림으로 살펴보자.
예를 들어 $N = 4$일 때의 경우를 살펴보자.
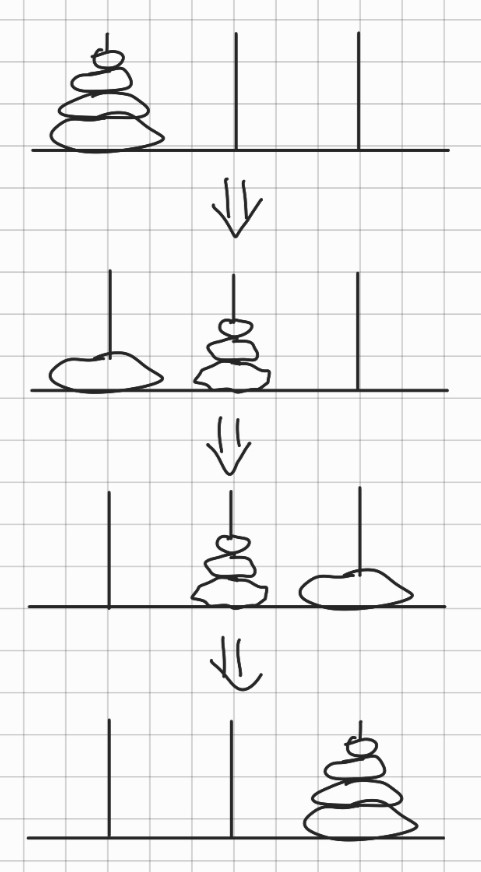
그림을 보면, 먼저 판 3개를 가운데 막대(2번)로 움직이고, 가장 큰 4번째 판을 오른쪽(3번)으로 움직인 후에, 다시 판 3개를 오른쪽(3번)으로 움직인다는 사실을 알 수 있다.
이를 통해, 우리는 $move(N, start, end)$라는 함수 하나를 정의할 것이다.
이 함수는 세 개의 인자를 받는다.
하나는 움직이는 판의 개수 $N$, 나머지 두 개는 판을 어디 막대에서 어디 막대로 옮길 것인지에 대한 막대 번호 $start$와 $end$이다.
예를 들자면, $move(4, 1, 3)$은 4개의 원판이 연속으로 있는 상황에서 4개의 원판을 막대 $1$에서 막대 $3$으로 옮기라는 뜻이다.
이 함수를 통해 위 그림의 상황을 나타내자면 다음과 같다.
$$move(4, 1, 3) = move(3, 1, 2) + print(1, 3) + move(3, 2, 3)$$
전형적인 재귀 함수의 모습이 완성되었다.
위의 예시를 조금 더 발전시켜 이 함수의 일반화를 해보자.
판 3개를 막대 $1$에서 막대 $2$로 옮기려면 어떻게 해야 할까?
위에 있는 판 2개를 막대 $1$에서 막대 $3$으로 옮긴 후, 맨 밑에 있는 판을 막대 $1$에서 $2$로 옮기고, 다시 이미 옮겼던 판 2개를 막대 $3$에서 막대 $2$로 옮겨야만 한다.
$$move(3, 1, 2) = move(2, 1, 3) + print(1, 2) + move(2, 3, 2)$$
규칙이 잘 보이지 않는다. 한 번만 더 해보자.
이제 판 $3$개를 막대 $2$에서 막대 $3$으로 옮기려면 어떻게 해야 할까?
위에 있는 판 2개를 막대 $2$에서 막대 $1$로 옮긴 후에, 맨 밑에 있는 판을 막대 $2$에서 $3$으로 옮기고, 다시 이미 옮겼던 판 2개를 막대 $1$에서 막대 $3$으로 옮겨야만 한다.
$$move(3, 2, 3) = move(2, 2, 1) + print(2, 3) + move(2, 1, 3)$$
이를 일반화하면, 일단 $N$개의 판을 $start$에서 $end$로 옮긴다고 한다면, 위에 있는 $N-1$개의 판을 $start$에서 $start$도 아니고 $end$도 아닌 제3의 지역($mid$)으로 옮긴 다음, 맨 밑의 판을 $start$에서 $end$로 옮기고, 이후, 다시 $N-1$개의 판을 $mid$에서 $end$로 옮겨야 된다.
$$move(N, start, end) = move(N-1, start, mid) + print(start, end) + move(N-1, mid, end)$$
그렇다면, $mid$는 어떤 식으로 표현이 될까?
여기서는 막대가 $1, 2, 3$으로만 표현이 되므로 $start$와 $end$를 제외한 막대의 번호 $mid$는 $6-start-end$로 표현할 수 있다.
이를 이용하면 완전하게 표현할 수 있다.
이 재귀 함수의 종료 조건을 생각해봐야 하는데, 판이 1개인 경우 그냥 그 판을 시작점에서 끝점으로 옮길 수 있으므로 그냥 $print(start, end)$를 해주고 종료해주면 된다.
이를 토대로 재귀적 구현을 해주면 된다.
판이 옮겨진 횟수 $K$는 잘 알려진 사실대로 $2^{N} - 1$을 출력해도 되고, 위의 $move$함수에 $print$를 몇 번 호출했나 카운트해주는 전역 변수를 하나 세워서 실제로 세어보는 것도 괜찮다.
아래는 내가 위의 접근 방식과 같이 작성한 파이썬 코드이다. 더보기를 누르면 확인할 수 있다.
# 11729번 하노이 탑 이동 순서
# 재귀
def move(N, start, end):
mid = 6 - start - end
if N == 1:
print(start, end)
return
move(N-1, start, mid)
print(start, end)
move(N-1, mid, end)
return
N = int(input())
print(2**N - 1)
move(N, 1, 3)'알고리즘 > 백준 문제 풀이' 카테고리의 다른 글
| [Python] 4179번 불! (0) | 2022.11.29 |
|---|---|
| [Python] 5427번 불 (0) | 2022.11.29 |
| [Python] 2036번 수열의 점수 / 1744번 수 묶기 (0) | 2022.11.28 |
| [Python] 17430번 가로등 (0) | 2022.11.23 |
| [Python] 1584번 게임 (0) | 2022.11.23 |